1 INLEIDING


 De Britse actuariële beroepsvereniging heeft recent een rapport uitgebracht over, wat zij noemen, “the Great Risk Transfer” (IFoA, 2021). Zij signaleren een maatschappelijke trend waarbij risico’s van instellingen –zoals werkgevers, de overheid en financiële dienstverleners– worden overgedragen aan individuen. Voorbeelden van deze trend zijn onder meer de vergaande verschuiving van defined benefit pensioenregelingen (DB) naar beschikbare premieregelingen (DC) en minder beleggingsproducten met garanties. In Nederland is deze ontwikkeling ook duidelijk gaande. Met het op handen zijnde nieuwe pensioenakkoord stappen alle pensioenfondsen en verzekeraars voor toekomstige pensioenopbouw over naar een premieovereenkomst met leeftijdsafhankelijk beleggingsbeleid. Het gevolg hiervan is dat er meer risico en onzekerheid over de hoogte van het opgebouwde pensioenvermogen bij de deelnemers komt te liggen. Een deel van deze toegenomen onzekerheid poogt men op te vangen in het nieuwe pensioenakkoord door de invoering van een solidariteitsreserve. De effectiviteit van deze reserve wordt elders in dit blad besproken door Van Bilsen, Mehlkopf en Pelsser.
De Britse actuariële beroepsvereniging heeft recent een rapport uitgebracht over, wat zij noemen, “the Great Risk Transfer” (IFoA, 2021). Zij signaleren een maatschappelijke trend waarbij risico’s van instellingen –zoals werkgevers, de overheid en financiële dienstverleners– worden overgedragen aan individuen. Voorbeelden van deze trend zijn onder meer de vergaande verschuiving van defined benefit pensioenregelingen (DB) naar beschikbare premieregelingen (DC) en minder beleggingsproducten met garanties. In Nederland is deze ontwikkeling ook duidelijk gaande. Met het op handen zijnde nieuwe pensioenakkoord stappen alle pensioenfondsen en verzekeraars voor toekomstige pensioenopbouw over naar een premieovereenkomst met leeftijdsafhankelijk beleggingsbeleid. Het gevolg hiervan is dat er meer risico en onzekerheid over de hoogte van het opgebouwde pensioenvermogen bij de deelnemers komt te liggen. Een deel van deze toegenomen onzekerheid poogt men op te vangen in het nieuwe pensioenakkoord door de invoering van een solidariteitsreserve. De effectiviteit van deze reserve wordt elders in dit blad besproken door Van Bilsen, Mehlkopf en Pelsser.
Gegeven de inherente onzekerheid over de hoogte van het opgebouwde pensioenvermogen in het nieuwe pensioencontract is het extra van belang dat pensioenfondsen op basis van doelstelling en risico-aversie van de deelnemers een optimaal beleggingsbeleid bepalen dat passend is voor de deelnemers in het fonds. Op dit moment doen pensioenfondsen al onderzoek naar de risico-aversie van de deelnemers en toetsen ze of het gevoerde beleggingsbeleid passend is voor het fonds als geheel. Bij de meeste fondsen wordt het beleggingsbeleid geëvalueerd binnen het kader van de standaard life-cycle beleggingstheorie van Merton (1969).
DE VRAAG RIJST DAN OOK OF DE PENSIOENSECTOR NIET BEZIG IS OM NOG NAUWKEURIGER HET VERKEERDE BELEGGINGSBELEID VOOR DE DEELNEMERS TE BEPALEN
Het probleem met deze aanpak is, in onze ogen, dat men hiermee te gemakkelijk voorbijgaat aan de fundamentele onzekerheden in het vaststellen van de risico-aversie van de deelnemers. De theorie van Merton maakt bijzonder sterke en specifieke aannames over de risico-aversie van deelnemers. De uitkomst van het “optimale” beleggingsbeleid is bijzonder gevoelig voor deze zeer specifieke aannamen. De vraag rijst dan ook of men niet bezig is om nog nauwkeuriger het verkeerde beleggingsbeleid voor de deelnemers te bepalen door binnen de kaders van de Merton-theorie blijven.
Wij willen daarom in dit artikel proberen om buiten de gebaande paden van de Merton-theorie te stappen. Onze ambitie is om te verkennen hoe we recht kunnen doen aan de fundamentele onzekerheden in deelnemerskenmerken, en desondanks toch een passend beleggingsbeleid aan te bieden voor de deelnemers. Daartoe vatten we in sectie 2 kort de standaard life-cycle beleggingstheorie samen. In sectie 3 gaan we dieper in op het uitvoeren van leeftijdsafhankelijk beleggingsbeleid in de praktijk. In sectie 4 bespreken we de invloed van fundamentele onzekerheid in de risico-aversie van deelnemers op het optimale beleggingsbeleid. We laten zien dat aangepaste beleggingsbeleid een geheel andere structuur heeft dan in het standaard Merton-model. Het aangepaste beleid is er expliciet op gericht om te proberen toe te beleggen naar een door de deelnemer gewenst referentiepunt en is er ook op gericht om extreme uitschieters (naar boven en naar beneden) te vermijden. Tenslotte concluderen we in sectie 5 dat we hiermee een grotere mate van zekerheid kunnen bieden aan elke deelnemer aangaande het te bereiken pensioenkapitaal ten opzichte van het standaard beleggingsbeleid in het Merton-model.
2 LEEFTIJDSAFHANKELIJK BELEGGINGSBELEID IN DE THEORIE
We herhalen kort de theoretische onderbouwing van het optimale beleggingsbeleid voor de deelnemers van een pensioenfonds op basis van het standaard lifecycle-model van Merton (1969). We nemen aan dat de deelnemer begint te werken op t=0 en op een vast tijdstip T (bijvoorbeeld T=40) met pensioen gaat. Voor de eenvoud gaan we ervan uit dat deze deelnemer met zekerheid de pensioendatum T bereikt. Tijdens haar werkzame leven betaalt ze op elk tijdstip t een premie aan haar pensioenfonds. Het pensioenfonds belegt deze premies om een kapitaal bij pensionering op te bouwen. De deelnemer wil haar premies zo goed mogelijk beleggen. Merton (1969) heeft laten zien wat de expliciete oplossing is voor dit probleem. Echter, om tot die oplossing te komen maakt Merton een bijzonder sterke aanname over de risico-aversie van de deelnemer. De risico-aversie kwantificeert in hoeverre de deelnemer zich zorgen maakt over de onzekerheid in het op te bouwen pensioenkapitaal. De aanname die Merton maakt is dat de risico-aversie gelijk is aan een constante waarde g. Dit is een buitengewoon sterke aanname: ongeacht je leeftijd of hoe rijk of arm je bent, de model-aanname van Merton is dat je risico-aversie altijd hetzelfde blijft. Het moge duidelijk zijn dat dit een weinig realistische aanname is.
Voor een belegger met constante risico-aversie g is het optimaal om altijd een constant gedeelte (m – g)/(gs2) van het totale pensioenkapitaal te beleggen in zakelijke waarden, waarbij m het verwachte rendement op zakelijke waarden, s de volatilitieit van de beleggingen en g de risicovrije rente is. Bij een hoger verwacht rendement m wil je meer in zakelijke waarden beleggen; bij een hogere volatiliteit s van de rendementen wil je minder in zakelijke waarden beleggen. En als je als belegger meer risicoavers bent (hogere waarde van g), dan wil je ook minder risicovol beleggen. In kwalitatieve zin zijn deze uitkomsten erg aansprekend en dat verklaart ook de brede acceptatie van het Merton-model. Echter, de exacte uitkomsten van het model worden in hoge mate bepaald door de onrealistische aanname dat de risico-aversie altijd constant is.
Hoe komen we op basis van een beleggingsbeleid met een constant gedeelte beleggen in zakelijke waarden nu uit bij een life-cycle beleggingsbeleid waarbij het gedeelte belegd in zakelijke waarden afneemt naarmate we dichter bij de pensioendatum komen? Dat komt door het begrip totaal pensioenkapitaal. Dit is gedefinieerd als de contante waarde op ieder tijdstip t van het te bereiken pensioenkapitaal op pensioendatum T. Dit totale bedrag kunnen we in twee stukken opknippen:
- Het opgebouwde financieel kapitaal op basis van de pensioenbijdragen die zijn betaald tussen tijdstip 0 en t en de reeds daarop behaalde beleggingsrendementen.
- De contante waarde van de nog te betalen pensioenpremies tussen t en T. Deze component wordt ook wel het menselijk kapitaal genoemd.
DE OPTIMALE LIFE-CYCLE BELEGGINGSSTRATEGIE PRESTEERT NOGAL SLECHT IN DE ECHTE WERELD, OMDAT DE ECHTE WERELD ER ANDERS UITZIET DAN DE AANNAMEN VAN HET MODEL
Naarmate de tijd vordert, wordt het financieel kapitaal steeds groter en het menselijk kapitaal steeds kleiner. De optimale Merton-strategie is om een constant gedeelte van het totale pensioenkapitaal in zakelijke waarden te beleggen. Gemeten ten opzichte van het financieel kapitaal, begin je daarom met een groot gedeelte in zakelijke waarden te beleggen. Naarmate t groter wordt, zet je een steeds groter gedeelte van het menselijk kapitaal om in financieel kapitaal en daalt de verhouding tussen het bedrag belegd in zakelijke waarden ten opzichte van het opgebouwde financieel kapitaal. Dat verklaart dus de dalende trend in zakelijke waarden bij de life-cycle beleggingsstrategie.
3 LEEFTIJDSAFHANKELIJK BELEGGINGSBELEID IN DE PRAKTIJK
De inrichting van leeftijdsafhankelijk beleggingsbeleid in de praktijk in Nederland leunt op de Merton-theorie. Uitgaande van economische verwachtingen en karakteristieken van de deelnemers zoekt men een “optimale” beleggingsstrategie. Daarbij spelen de nodige onzekerheden een rol, zoals onzekerheden in de economie en ook onzekerheden over deelnemerskarakteristieken zoals risico-aversie.
Het vaststellen van een beleggingsbeleid met onzekerheid over de toekomstige economische omstandigheden is in de Nederlandse pensioenpraktijk inmiddels gemeengoed. Afgelopen jaren zetten pensioenfondsen hier flinke stappen. Voorheen werkte men vaak met één economische scenario-set, waarbinnen werd geoptimaliseerd. Tegenwoordig gebruiken pensioenfondsen economische scenario’s inclusief stressscenario’s. Daarbinnen zoeken ze naar een beleggingsbeleid dat een goede performance blijft geven onder meerdere economische scenario’s inclusief stressscenario’s.
3.1 ONZEKERHEID OVER RISICO-AVERSIE
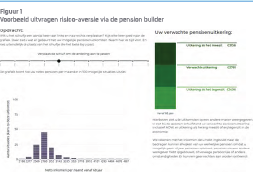 Waar we minder aandacht voor zien in de praktijk zijn onzekerheden over de juiste specificatie van risico-aversie van de deelnemer. Vaak hanteert men de aanname van constante risico-aversie als noodzakelijke en bepalende inputvariabele voor de optimale beleggingsstrategie. Pensioenfondsen zijn verplicht de risico-aversie van de deelnemer uit te vragen of te veronderstellen. Alhoewel hiervoor meerdere technieken zijn ontwikkeld zoals bijvoorbeeld loterijvragen of de pension builder (Donkers e.a., 2016), is het uitvragen van deze informatie in de praktijk niet eenvoudig.
Waar we minder aandacht voor zien in de praktijk zijn onzekerheden over de juiste specificatie van risico-aversie van de deelnemer. Vaak hanteert men de aanname van constante risico-aversie als noodzakelijke en bepalende inputvariabele voor de optimale beleggingsstrategie. Pensioenfondsen zijn verplicht de risico-aversie van de deelnemer uit te vragen of te veronderstellen. Alhoewel hiervoor meerdere technieken zijn ontwikkeld zoals bijvoorbeeld loterijvragen of de pension builder (Donkers e.a., 2016), is het uitvragen van deze informatie in de praktijk niet eenvoudig.
Veel deelnemers nemen automatisch deel aan een pensioenregeling en zijn moeilijk te activeren om vragen te beantwoorden. Hierdoor is het vaak lastig voldoende inputgegevens te bemachtigen over hun risico-aversie. Het ontbreken van deze gegevens dwingt pensioenfondsen om voor veel deelnemers bij de bepaling van de optimale beleggingsstrategie uit te gaan van een veronderstelde constante waarde voor de risico-aversie.
DOOR HET BELEGGINGSBELEID ZODANIG IN TE RICHTEN DAT WE EXPLICIET TOEWERKEN NAAR EEN GEWENST REFERENTIEPUNT IS HET MOGELIJK OM EEN GROTERE MATE VAN ZEKERHEID TE BIEDEN AAN ELKE DEELNEMER AANGAANDE HET TE BEREIKEN PENSIOENKAPITAAL
Ook als deelnemers wel de vragen en gegevens over hun risico-aversie beantwoorden, bestaat er nog steeds onzekerheid over de juistheid van de uitkomsten. Een online uitvraag kan niet te lang en gedetailleerd zijn. Je loopt dan het risico dat deelnemers vroegtijdig afhaken, waardoor je mogelijk helemaal geen informatie inwint. Ook kunnen behavorial biases van invloed zijn op de uitkomsten, bijvoorbeeld de vormgeving van keuzearchitectuur (Thaler en Sunstein, 2008). Zo hebben deelnemers veelal de neiging om de middelste optie te kiezen of een positie die relatief is aan het midden. Ook kan een vooraf ingevulde default sturend zijn. Bij vragenlijsten is er een risico op framing in de teksten die van invloed kunnen zijn op de uitkomsten.
Daarboven komt de vraag of deelnemers überhaupt iets kunnen zeggen over hun risico-aversie voor de lange termijn. Dat is een heel andere vraag dan de risico-aversie voor een loterij die typisch gaat over de korte termijn.
Ondanks verbeterde methodes van uitvragen, toegenomen ervaring en het gebruik van nieuwe technieken blijft het in de praktijk lastig om alle benodigde informatie van een deelnemer uit te vragen of om deelnemers te activeren toegang tot deze gegevens te verlenen. Als gevolg hiervan moeten we accepteren dat er bij een individuele deelnemer fundamentele onzekerheid blijft bestaan over de juistheid van de gehanteerde risico-aversie.
4 OMGAAN MET ONZEKERHEID IN RISICO-AVERSIE
Hoe kunnen we recht doen aan de fundamentele onzekerheid ten aanzien van de risico-aversie van deelnemers bij het vaststellen van een passend beleggingsbeleid? Met andere woorden, hoe kunnen we “ongeveer het goede beleggingsbeleid” vaststellen voor een deelnemer in plaats van “nog nauwkeuriger het verkeerde beleggingsbeleid” gebaseerd op de evident verkeerde aanname van constante risico-aversie?
Om tot een antwoorde te komen, passen we de robustness aanpak uit de academische literatuur (Hansen en Sargent, 2007) toe op de onzekerheid in de specificatie van de risico-aversie. We onderzoeken dus in hoeverre we de theorie van Merton kunnen uitbreiden om recht te doen aan de fundamentele onzekerheid in de specificatie van de risico-aversie. De model-aanname van constante risico-aversie is evident foutief in de echte wereld, en leidt daarom tot model-onzekerheid voor het Merton-model.
4.1 GEEN REKENING HOUDEN MET MODEL-ONZEKERHEID MAAKT BELEID FRAGIEL VOOR AANNAMES
Wanneer we geen rekening houden met de model-onzekerheid in het Merton-model, dan heeft de “optimale” investeringsstrategie de neiging om fragiel te zijn. De optimale beleggingsstrategie van het Merton-model is erg gevoelig is voor kleine aanpassingen in de model-specificaties: de constante fractie belegd in zakelijke waarden is een gevolg van de model-aanname van constante risico-aversie. Voor praktische toepassingen betekent dit dat in veel gevallen de beste oplossing binnen het model nogal slecht presteert in de echte wereld, omdat de echte wereld er anders uitziet dan de model-aannamen. Dit is een bekend zwak punt van “niet-robuuste” optimalisatie, zie bijvoorbeeld Hansen en Sargent (2007).
4.2 AANGEPASTE NUTSFUNCTIE DOOR MODEL-ONZEKERHEID
 We nemen de onzekerheid in de specificatie van de risico-aversie expliciet mee door een robuuste optimalisatie-methode te gebruiken. Het idee is dat we het Merton-model niet beschouwen als de ultieme waarheid, maar als een initiële inschatting. We erkennen dus expliciet dat er alternatieve specificaties van de risico-aversie mogelijk zijn. Hansen en Sargent (2007) stellen voor om de robuuste optimalisatie te implementeren als een spel met twee spelers waarin beide spelers elkaar tegenwerken. De eerste speler zoekt naar een optimaal beleggingsbeleid. De tegenspeler kiest een zo ongunstig mogelijke aanname voor de risico-aversie, waarbij de tegenspeler haar keuze aanpast aan het beleggingsbeleid van de eerste speler om tot de slechtst mogelijk uitkomst te komen voor de eerste speler. De eerste speler is zich bewust van de acties van de tegenspeler en probeert daarom een beleggingsbeleid te kiezen dat nog steeds een goed resultaat oplevert, maar zo min mogelijk kwetsbaar is voor een verkeerde keuze in de aanname van de risico-aversie. De formulering als een twee-speler spel leidt daarom tot een “robuuste” uitkomst voor het beleggingsbeleid en dat is precies waar we naar op zoek zijn.
We nemen de onzekerheid in de specificatie van de risico-aversie expliciet mee door een robuuste optimalisatie-methode te gebruiken. Het idee is dat we het Merton-model niet beschouwen als de ultieme waarheid, maar als een initiële inschatting. We erkennen dus expliciet dat er alternatieve specificaties van de risico-aversie mogelijk zijn. Hansen en Sargent (2007) stellen voor om de robuuste optimalisatie te implementeren als een spel met twee spelers waarin beide spelers elkaar tegenwerken. De eerste speler zoekt naar een optimaal beleggingsbeleid. De tegenspeler kiest een zo ongunstig mogelijke aanname voor de risico-aversie, waarbij de tegenspeler haar keuze aanpast aan het beleggingsbeleid van de eerste speler om tot de slechtst mogelijk uitkomst te komen voor de eerste speler. De eerste speler is zich bewust van de acties van de tegenspeler en probeert daarom een beleggingsbeleid te kiezen dat nog steeds een goed resultaat oplevert, maar zo min mogelijk kwetsbaar is voor een verkeerde keuze in de aanname van de risico-aversie. De formulering als een twee-speler spel leidt daarom tot een “robuuste” uitkomst voor het beleggingsbeleid en dat is precies waar we naar op zoek zijn.
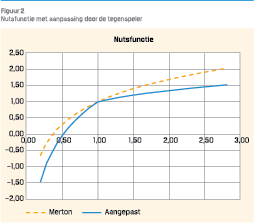
Een groot voordeel van robuuste optimalisatie is dat we een grote verzameling van alternatieve modellen naast het Merton-model in ogenschouw nemen. We kijken niet alleen naar het verkeerd kiezen van een constante risico-aversie parameter g, maar juist ook naar alternatieve modellen met niet-constante risico-aversie. We kijken expliciet naar een grotere klasse van alternatieve modellen voor het Merton-model, in plaats van alleen parameter-onzekerheid omtrent de risico-aversie parameter g. Als we starten vanuit het Merton-model als initiële aanname, dan lijkt het voor de eerste speler, door de “tegenwerking” van de tegenspeler, alsof de nutsfunctie van de deelnemer een “knik” krijgt. In termen van risico-aversie betekent dit dat we het robuuste beleggingsbeleid niet baseren op het Merton-model met een constante risico-aversie, maar op een model met een “piek” in de risico-aversie op een bepaald punt. Een voorbeeld van een dergelijke “geknikte” nutsfunctie is te zien in figuur 1.
De oranje gestippelde lijn is de nutsfunctie van het Merton-model met constante risico-aversie. De blauwe doorgetrokken lijn geeft de door de tweede speler “aangepaste” nutsfunctie weer die een knik vertoont.
Het economische gevolg van een dergelijke “knik” in de nutsfunctie is dat de deelnemer (veel) meer risico-avers wordt rond het punt waar de knik zit. We zien dus dat we door de robuuste optimalisatie-techniek uitkomen op een nieuw soort nutsfunctie (met knik) die buiten het standaard Merton-model ligt. We kunnen de knik in de nutsfunctie van de deelnemer interpreteren als een referentiepunt in het te bereiken pensioenkapitaal dat zij graag wil bereiken en vasthouden. Als gevolg hiervan, krijgt het robuuste optimale beleggingsbeleid een geheel andere structuur dan in het Merton-model. Het robuuste beleid is erop gericht om te proberen toe te beleggen naar het door de deelnemer gewenste referentiepunt en is er ook op gericht om extreme uitschieters (naar boven en naar beneden) te vermijden. Met andere woorden, het robuuste beleggingsbeleid probeert om de kans zo groot mogelijk te maken om het referentiepunt te bereiken.
Voor economische scenario’s waarin het geprojecteerde pensioenkapitaal onder het referentiepunt ligt, is de robuuste optimale strategie het nemen van meer beleggingsrisico in een poging om het gewenste referentiepunt te bereiken op de pensioendatum. Als het referentiepunt (naar verwachting) kan worden behaald, is het verstandig om te de-risken om op die manier het behaalde beleggingsresultaat veilig te stellen. Voor economische scenario’s waarin het geprojecteerde vermogen boven de benchmark ligt, is het wederom optimaal om meer beleggingsrisico te nemen om extra rendement te behalen zonder daarbij het referentiepunt in gevaar te brengen.
4.3 ILLUSTRATIE ROBUUSTHEID EN NUTSVERLIES DOOR HANTEREN VERKEERDE NUTSFUNCTIE
Wat is nu het voordeel van het volgen van het “robuuste” beleggingsbeleid ten opzichte van de standaard life-cycle? De standaard life-cycle is alleen maar optimaal als we de juiste nutsfunctie van de deelnemer exact weten. Als we een fout maken bij het vaststellen van de risico-aversie, dan voeren we het verkeerde beleggingsbeleid uit voor de deelnemer hetgeen leidt tot een suboptimale uitkomst voor de deelnemer.
Om meer inzicht te krijgen op de invloed van een fout in het vaststellen van de risico-aversie, kunnen we de volgende berekening maken. Stel een deelnemer heeft een “ware” (constante) risico-aversie g*, maar deze juiste waarde kennen we niet. In plaats daarvan voeren we een beleggingsbeleid uit op basis van een geschatte waarde g. Voor elke waarde g ≠ g*, leidt de verkeerde inschatting van g tot een suboptimaal beleggingsbeleid en daarmee tot een verlies van nut voor de deelnemer. De grootte van het verloren nut drukken we uit in een zekerheidsequivalent (“certainty equivalent”) in termen van equivalent verlies in beleggingsrendement per jaar.
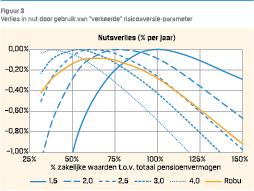 De uitkomsten van deze berekeningen zijn weergegeven in figuur 3. Op de horizontale as zien we het (constante) percentage geïnvesteerd in zakelijke waarden relatief ten opzichte van het totale pensioenvermogen. Op de verticale as zien we het nutsverlies uitgedrukt in verlies in beleggingsrendement per jaar. De blauw gestippelde lijnen geven telkens het nutsverlies voor een Merton-beleggingsstrategie voor waarden van de risico-aversie parameter g variërend van 1.5 tot 4. Elke blauwe lijn tikt het niveau van 0% nutsverlies aan wanneer de beleggingsmix aansluit bij de model-parameter g* voor die lijn. We zien echter ook dat elke blauwe lijn steeds wegzakt onder 0% als de beleggingsmix afwijkt van de model-waarde.
De uitkomsten van deze berekeningen zijn weergegeven in figuur 3. Op de horizontale as zien we het (constante) percentage geïnvesteerd in zakelijke waarden relatief ten opzichte van het totale pensioenvermogen. Op de verticale as zien we het nutsverlies uitgedrukt in verlies in beleggingsrendement per jaar. De blauw gestippelde lijnen geven telkens het nutsverlies voor een Merton-beleggingsstrategie voor waarden van de risico-aversie parameter g variërend van 1.5 tot 4. Elke blauwe lijn tikt het niveau van 0% nutsverlies aan wanneer de beleggingsmix aansluit bij de model-parameter g* voor die lijn. We zien echter ook dat elke blauwe lijn steeds wegzakt onder 0% als de beleggingsmix afwijkt van de model-waarde.
De oranje lijn geeft het nutsverlies weer voor de robuuste beleggingsstrategie waarbij we expliciet proberen om een referentiepunt te behalen voor de deelnemer. We zien hierbij twee dingen. Ten eerste tikt de oranje lijn nooit het niveau van 0% aan. Dat willen zeggen dat de robuuste strategie voor geen enkele deelnemer met een echt constante risico-aversie optimaal is. Aan de andere kant zien we ook dat de oranje lijn minder snel naar beneden zakt bij afwijkingen in de beleggingsmix ten opzichte van de blauwe lijnen. Dat wil zeggen dat voor een (relatief) groot interval van deelnemers de robuuste strategie “bij benadering goed” is en daarmee minder gevoelig is voor een verkeerde specificatie van de (niet-constante) risico-aversie. Dit is precies het effect dat we met de robuuste optimalisatie hoopten te bereiken.
5 CONCLUSIES
We begonnen dit artikel met de, onder andere door de Britse actuarissen, gesignaleerde maatschappelijke trend van het meer en meer risico neerleggen bij individuen. Met het op handen zijnde nieuwe pensioenakkoord stappen we nog verder over naar premieregelingen met als gevolg dat er meer risico en onzekerheid over de hoogte van het opgebouwde pensioenvermogen bij de deelnemers komt te liggen. Veel pensioenfondsen gaan uit van de standaard life-cycle beleggingstheorie van Merton (1969). Echter, de theorie van Merton maakt bijzonder sterke en specifieke aannames over de risico-aversie van deelnemers. De vraag rijst dan ook of we niet bezig zijn om nog nauwkeuriger het verkeerde beleggingsbeleid voor de deelnemers te bepalen door binnen de kaders van de Merton-theorie blijven.
We hebben in dit artikel een poging gedaan om te verkennen hoe we recht kunnen doen aan de fundamentele onzekerheden in deelnemerskenmerken en desondanks toch een passend beleggingsbeleid te bieden voor de deelnemers. Door gebruik te maken van een robuuste optimalisatie van het beleggingsbeleid houden we expliciet rekening met de fundamentele onzekerheid aangaande de risico-aversie van elke deelnemer. We vinden dat het robuuste optimale beleggingsbeleid een geheel andere structuur heeft dan in het standaard Merton-model. Het robuuste beleid is er expliciet op gericht om te proberen toe te beleggen naar een door de deelnemer gewenst referentiepunt en is er ook op gericht om extreme uitschieters (naar boven en naar beneden) te vermijden. Met andere woorden, het robuuste beleggingsbeleid probeert de kans zo groot mogelijk te maken om het referentiepunt te bereiken, zonder daarbij harde garanties te geven. We zien daarmee dat deze vorm van robuust beleggingsbeleid tegemoetkomt aan het mitigeren van de onzekerheid voor de individuele deelnemer en dus een tegenwicht kan bieden tegen de ongewenste neveneffecten van de risico-overdracht naar individuen. Door het beleggingsbeleid zodanig in te richten dat we expliciet toewerken naar een gewenst referentiepunt is het mogelijk om (zonder harde garanties te bieden) toch een grotere mate van zekerheid te bieden aan elke deelnemer aangaande het te bereiken pensioenkapitaal.
Referenties
- Donkers, B., Dellaert, B., Vermeulen, E., Turlings, M. & Steenkamp, T. (2016). Naar een nieuwe aanpak voor risicoprofielmeting voor deelnemers in pensioenregelingen. Netspar.
- Hansen, L., & Sargent, T. (2007). Robustness. Princeton University Press.
- Institute and Faculty of Actuaries (IFoA) (2021), The Great Risk Transfer: Campaign Recommendations, www.actuaries.org.uk
- Merton, R. (1969). Lifetime portfolio selection under uncertainty: The continuous-time case. The Review of Economics and Statistics, 51(3), 247-257.
- Richard H. Thaler, Cass R. Sunstein (2008), Nudge: Improving decisions about health, wealth, and happiness. Yale University Press.
Noten
- Dit artikel is een ingekorte en bewerkte versie van Netspar Design Paper 174 met de titel Beleggingsbeleid bij onzekerheid over risicobereidheid en budget. Het volledige paper is te downloaden via www.netspar.nl.
in VBA Journaal door Agnes Joseph, Antoon Pelsser en Lieke Werner
