In het nieuwe pensioenstelsel gaan we naar een leeftijdsafhankelijk beleggingsbeleid. Voor ieder leeftijdscohort moet het beleggingsbeleid worden vastgesteld, hieruit volgt het beleggingsbeleid over het leven: de lifecycle. Maar hoe komen we tot deze lifecycle? Een vuistregel die vaak genoemd wordt is dat de blootstelling naar zakelijke waarden gelijk moet zijn aan ‘100 min de leeftijd’. Oftewel, een jongere van 30 belegd 70% in zakelijke waarden en iemand van 70 belegd 30% in zakelijke waarden. In dit artikel vergelijken we deze vuistregel met een vaste 50/50 mix en een geoptimaliseerde lifecycle. Voegt de extra complexiteit van een optimalisatie voldoende waarde toe, of volstaat een van de eenvoudigere lifecycles?
De twee belangrijkste elementen die moeten worden vastgesteld in een lifecycle zijn de blootstelling naar zakelijke waarden en de renteafdekking voor elke leeftijd. Hiervoor is het natuurlijk wel van belang hoe de zakelijke waarden en de renteafdekking worden ingevuld. In de solidaire premieregeling gaat de zakelijke waarden blootstelling via het overrendement en heeft iedereen blootstelling aan dezelfde ‘overrendementsportefeuille’, daarnaast wordt er een perfecte renteafdekking bijgeschreven, afhankelijk van de renteafdekking die van te voren is vastgesteld voor een leeftijdscohort.1 In de flexibele premieregeling kan voor ieder leeftijdscohort apart een beleggingsmix worden vastgesteld. Maar ook hier is het vaak gewenst om de analyse te beperken tot de renteafdekking en een of twee overrendementsportefeuilles om complexiteit te beperken. In een eerder artikel2 keken we naar de gewenste renteafdekking in de lifecycle, in dit artikel beperken we ons tot de blootstelling naar zakelijke waarden (overrendement).
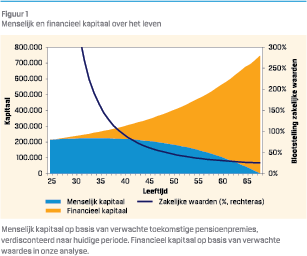Voor de blootstelling naar zakelijke waarden in de lifecycle wordt vaak ‘100 min leeftijd’ aangehaald (bijv. Bodie & Crane, 1997). Het idee hierachter volgt uit de ontwikkeling van menselijk kapitaal over het leven. Mensen hebben zowel menselijk kapitaal (toekomstig verdienvermogen) als financieel kapitaal (bijvoorbeeld het opgebouwde pensioenvermogen). Als iemand ouder wordt neemt normaal gesproken zijn menselijk kapitaal af, terwijl het financieel kapitaal toeneemt. In dit geval moet bij het ouder worden steeds minder risico genomen worden binnen het financieel kapitaal, zodat de totale blootstelling naar risico’s zoveel mogelijk gelijk blijft over het leven (Bodie, Merton & Samuelson, 1992). De aanname hierbij is dat menselijk kapitaal minder risicovol is, of in ieder geval niet sterk samenhangt met financiële markten. Oftewel, een jong iemand heeft veel menselijk kapitaal (met weinig risico) en weinig financieel kapitaal. Om over het gehele kapitaal tot de gewenste mate van risico te komen moet dus relatief veel risico genomen worden binnen het menselijk kapitaal.3 Voor een oudere is dit precies omgekeerd. Dit is ook geïllustreerd in figuur 1. In deze figuur is het gewicht zakelijke waarden getoond binnen het financieel kapitaal om 25% blootstelling te geven over het totale kapitaal (menselijk + financieel kapitaal).
Als deze blootstelling wordt aangehouden is de absolute blootstelling naar zakelijke waarden relatief constant over het leven. Hierdoor is er optimale diversificatie over tijd wat leidt tot een efficiënte risico-rendementsverhouding. Voor de jongsten zou dit echter een enorm hoge mate van leverage betekenen, omdat het financieel kapitaal – de noemer in de berekening – nog heel laag is. Dit is in de meeste gevallen ongewenst vanwege de kans op een negatief kapitaal, de negatieve impact van risico op het geometrisch rendement en/of de mogelijke impact op het draagvlak van de pensioenregeling. Om die reden is de maximale blootstelling veelal afgekapt op 200% – 300%. Voor deze studie hanteren we een afkapping op 300%.4
Overigens zijn er ook stromingen in de literatuur die het concept van de dalende blootstelling naar zakelijke waarden bekritiseren. Onder andere Arnott, Sherrerd & Wu (2013) beargumenteren dat een stabiele mix, of zelfs een oplopend risicoprofiel, tot betere resultaten leidt, omdat meer risico genomen kan worden op het moment dat er veel vermogen is. Dit is wel afhankelijk van hoe – en wanneer – risico’s gemeten worden.
In tegenstelling tot een vaste mix houdt de ‘100 min leeftijd’ dus tot zekere mate rekening met de ontwikkeling van menselijk kapitaal. Echter wel op een weinig verfijnde manier. Zoals in figuur 1 ook is te zien volgt uit het menselijk kapitaal geen lineaire afbouw, maar vaak eentje die hard daalt op jonge leeftijden en daarna minder hard wanneer de leeftijd toeneemt. Daarnaast wordt geen rekening gehouden met de risicobereidheid van de deelnemer of het leeftijdscohort. Uit onderzoek (bijvoorbeeld Alserda et al., 2019) blijkt dat deelnemers – maar ook populaties van verschillende pensioenfondsen – verschillen in de mate dat ze risico’s willen nemen met hun (totale) pensioenuitkering. Door voor iedereen dezelfde lifecycle te gebruiken wordt welvaart misgelopen. Sommige deelnemers (populaties) nemen te weinig risico en anderen te veel. Dit kan deels opgelost worden door de algemene regel ‘100 min leeftijd’ om te zetten in ‘c min leeftijd’, waarbij c – het startniveau – afhangt van de risicobereidheid van de deelnemers of het leeftijdscohort. Hiermee blijft het relatief eenvoudig, maar wordt de potentie van een volledige optimalisatie nog steeds beperkt. Het andere alternatief is een volledige optimalisatie, hoewel daarvoor in de praktijk ook versimpelingen voor nodig zijn.5
Risico van menselijk kapitaal
Een belangrijk aandachtspunt binnen de lifecycle theorie is hoe om te gaan met risico’s binnen het menselijk kapitaal. Denk hierbij aan de kans op (langdurige) werkloosheid. Zo lang de kans op werkloosheid niet samenhangt met financiële markten dan is er voor een werkende geen impact op de optimale lifecycle. Voor mensen voor wie dit wel het geval is (bijvoorbeeld een beleggingsstrateeg) is de optimale allocatie naar zakelijke waarden normaal gesproken lager.
Voor deelnemers die stoppen met opbouwen binnen een regeling (de slapers) is de reden erg belangrijk. Indien ze in een andere regeling verder gaan met opbouwen hoeft dit geen gevolgen te hebben op de lifecycle als het nieuwe beleggingsbeleid min of meer aansluit bij de huidige lifecycle. Wanneer ze echter helemaal stoppen met werken – al dan niet vanwege arbeidsongeschiktheid – zorgt dit voor minder menselijk kapitaal en een minder risicovolle optimale mix. Dit is de reden waarom binnen de solidaire premieregeling er de mogelijkheid is om aparte toedelingsfactoren vast te stellen voor specifieke groepen, zoals slapers.
METHODE
Om de onderzoeksvraag te beantwoorden rekenen we verschillende lifecycles door in een simulatiemodel. We doen dit in drie stappen: 1) Een vaste mix, 2) ‘c min leeftijd’ lifecycle’ en 3) een – binnen bepaalde grenzen – geoptimaliseerde lifecycle.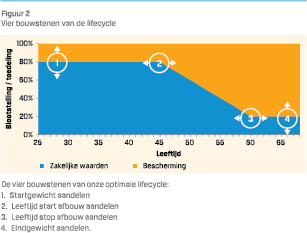
- Een vaste blootstelling naar zakelijke waarden, onafhankelijk van de leeftijd. We pakken hierbij de optimale vaste mix tussen 0% en 300% (301 varianten). Daarnaast analyseren we een vaste 50% mix als speciaal geval.
- Optimale ‘c min leeftijd’ lifecycle: Waarbij we ‘c’ variëren tussen 0% en 300% (301 varianten) en de variant kiezen die de hoogste verwachte welvaart oplevert. We hanteren een minimale blootstelling van 0%, dus negatieve blootstelling is niet mogelijk. Bij deze varianten analyseren we ‘100 min leeftijd’ als speciaal geval.
- Optimale lifecycle: We variëren de lifecycles aan de hand van vier bouwstenen: 1) Startgewicht aandelen, 2) leeftijd waarop wordt begonnen met afbouwen, 3) leeftijd waarop wordt geëindigd met afbouw en 4) eindgewicht aandelen. Dit is geïllustreerd in figuur 2. Tussen het start- en eindpunt interpoleren we de blootstelling naar aandelen. Door stappen van 10% in blootstelling en 1 jaar in leeftijd te gebruiken krijgen we in totaal ruim 600.000 varianten (met een logische afbouw). Hieruit selecteren we de variant die de hoogste verwachte welvaart oplevert.
Om complexiteit te beperken kijken we alleen naar een invulling van zakelijke waarden met aandelen. In de praktijk zullen er ook andere – veelal minder risicovolle – beleggingen opgenomen worden. In dat geval zal de optimale blootstelling naar zakelijke waarden hoger liggen, ter compensatie van het lagere risicorendementsprofiel. De renteafdekking houden we in alle varianten constant. Deze wordt van 0% in de laatste 20 jaar voor pensioen opgebouwd tot 100%.
Voor de analyse maken we gebruik van drie voorbeeld deelnemers die allemaal starten met opbouwen op 25-jarige leeftijd en op dat moment een salaris hebben van 25.000 euro per jaar. Het inkomen stijgt met inflatie en carrièregroei. Voor de deelnemers wordt 20% premie betaald over de pensioengrondslag (franchise start op 15.000 en stijgt met inflatie). Tijdens pensionering ontvangen de deelnemers een AOW uitkering die aan het begin van de analyse start op € 10.500 en daarna stijgt met inflatie.
De deelnemers verschillen in hun mate van risicobereidheid. Bert Bibber heeft een lage risicobereidheid (γ = 10), Dirk Dozijn heeft een gemiddelde risicobereidheid (γ = 3) en Vincent Vegas heeft een hoge risicobereidheid (γ = 1). Verwachte welvaart (nut) wordt berekent aan de hand van de volgende nutsfunctie: U(X) =1 – γ X1 – γ . Met U het nut, afhankelijk van X het totale pensioeninkomen en risico-aversie parameter γ.
Voor de doorrekening maken we gebruik van de door DNB aangeleverde scenario’s (10.000) op basis van het nieuwe commissie parameters (2022) model. Hier wordt gerekend met een gemiddelde 1-jaars rente van 1,2%, een gemiddelde 10-jaarsrente van 1,9% en een (geometrisch) gemiddeld aandelenrendement van 5,3%. In dit model wordt met behulp van stochastische volatiliteit tot zekere hoogte rekening gehouden met ‘dikke staarten’.
Laag risicoprofiel: Bert Bibber
Als eerste kijken we naar de resultaten voor de meest risico-averse deelnemer: Bert Bibber. De resultaten van de verschillende lifecycles staan in tabel 1. In deze en volgende tabellen kijken we naar vier variabelen. De verwachte uitkomst (mediaan), de slecht weer uitkomst (5% percentiel), de wettelijke definitie van de risicohouding (relatieve verschil tussen mediaan en slecht weer uitkomst) en de verwachte welvaart. De verwachte welvaart wordt gemeten op basis van de zekerheidsequivalent. Dit is de zekere pensioenuitkomst die hetzelfde welvaart oplevert als de distributie van mogelijke pensioenuitkomsten, rekening houdend met de relevante risicobereidheid.6
Van de vaste mixen leidt 42% gewicht naar zakelijke waarde de beste resultaten op. De optimale ‘c min leeftijd’ lifecycle is gelijk aan de ‘100 min leeftijd’ lifecycle. De verder geoptimaliseerde lifecycle – zie figuur 3 – begint aanzienlijk hoger (160%), maar bouwt vervolgens sneller af en eindigt op 10% blootstelling naar aandelen. Door de snellere afbouw wordt geprofiteerd van zowel een hogere startblootstelling als van een lagere blootstelling net voor pensioen. Uit de resultaten in tabel 1 blijkt duidelijk dat hierdoor een efficiënter risico-rendementsprofiel wordt behaald: De verwachte uitkering is hoger en het risico is lager, gemeten op basis van de hogere slecht weer uitkomst. Dit zorgt ervoor dat de verwachte welvaart 3% tot 7% hoger uitvalt dan voor de vuistregels.
Gemiddeld risicoprofiel: Dirk Dozijn
Deelnemer Dirk Dozijn vertegenwoordigd de gemiddelde deelnemer. We zien echter in tabel 2 dat de vuistregel ‘100 min leeftijd’ niet goed aansluit bij zijn (de gemiddelde) risicohouding. Een 52% hogere blootstelling zorgt voor betere resultaten in termen van verwachte welvaart. Ook de 50% vaste mix bevat te weinig risico, een vaste mix van 95% zakelijke waarden pakt beter uit.
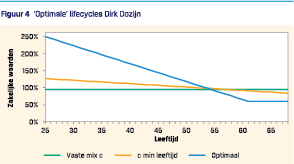
Een verder geoptimaliseerde lifecycle – zie figuur 4 – begint zelfs nog risicovoller (250%) en bouwt af tot 60% blootstelling naar aandelen. Dit leidt ook weer tot een efficiënter risico-rendementsprofiel (hoger slecht weer scenario en verwachte uitkomst) en daarmee tot welvaartswinsten (5% tot 17%).
Hoog risicoprofiel: Vince Vegas
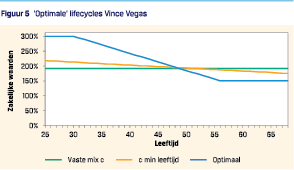
Ten slotte kijken we naar Vince Vegas. Zoals te verwachten zijn de lifecycles op basis van de vuistregels te risicomijdend voor deze deelnemer. Door zijn hoge risicotolerantie zou deze deelnemer bij voorkeur met hefboom in aandelen beleggen.
Ondanks een sterke impact op het slecht-weer scenario zorgt dit voor een grote stijging van het verwacht pensioen. Dit is voor deze deelnemer – vanwege zijn hoge risicotolerantie – het belangrijkste. Ook in dit geval zien we dat de meer optimale lifecycle leidt tot een efficiënter risicoprofiel en daarmee tot significante welvaartswinsten (tussen de 3% en 71%).
OPTIMALISATIE IS DE MOEITE WAARD
Uit de voorgaande analyses kunnen we twee conclusies trekken. Als eerste zien we dat het aanpassen van het beleggingsbeleid aan de risicohouding van de deelnemer veel meerwaarde kan bieden. Wat voor de ene deelnemer een efficiënt beleggingsbeleid is, bevat voor de andere deelnemer te veel of te weinig risico. Een koppeling tussen de risicohouding en het beleggingsbeleid levert daarmee welvaartswinsten op. Als tweede zien we dat een beperkte optimalisatie al substantiële welvaartswinsten kan opleveren tegenover de vaste mix en de versimpelde lifecycle (‘c min leeftijd’). Dit is vooral waar als we de geoptimaliseerde lifecycles vergelijken met de meest bekende vuistregels: ‘100 min leeftijd’ en een vaste 50% mix. Een optimalisatie is dus zeker de moeite en de extra complexiteit waard.
De exacte vorm van de lifecycle is uiteraard afhankelijk van de economische aannames die gehanteerd worden. Bovendien is het maar de vraag of een blootstelling (ruim) boven de 100% operationeel mogelijk is en/of gewenst is vanuit communicatie en draagvlak overwegingen. Desondanks zien we dat een efficiënt ontwerp van de lifecycle sterk kan bijdragen aan de (verwachte) welvaart die deelnemers uit hun pensioen gaan krijgen, dit vereist dan ook voldoende aandacht.
LIFECYCLES IN HET NIEUWE PENSIOENSTELSEL
In de nieuwe pensioenregelingen vormen lifecycles de basis van het beleggingsbeleid. In de solidaire premieregeling gaat het over toedeling naar overrendement en renteafdekking per leeftijdscohort, dat samen een (impliciete) lifecycle vormt. In de flexibele premieregeling is sprake van een of meerdere expliciete lifecycles, waar per leeftijd de blootstelling naar verschillende beleggingen wordt vastgesteld. Een belangrijk verschil tussen de twee regelingen is dat alleen bij de flexibele premieregeling keuzevrijheid kan worden geboden. Uit onze analyse blijkt dat dit meerwaarde kan bieden, maar alleen als deelnemers ook daadwerkelijk een keuze maken. Daarnaast zien we dat het ontwerp van de lifecycle erg belangrijk is. Voldoende aandacht voor de lifecycle is daarom essentieel voor een goed beleggingsbeleid in het nieuwe pensioenstelsel.
Literatuur
- Alserda, G. A., Dellaert, B. G., Swinkels, L., & van der Lecq, F. S. (2019). Individual pension risk preference elicitation and collective asset allocation with heterogeneity. Journal of Banking & Finance, 101, 206-225.
- Arnott, R. D., Sherrerd, K. F., & Wu, L. (2013). The Glidepath Illusion… and Potential Solutions The Journal of Retirement 1(2), 13-28.
- Bodie, Z., Merton, R. C., & Samuelson, W. F. (1992). Labor supply flexibility and portfolio choice in a life cycle model. Journal of economic dynamics and control, 16(3-4), 427-449.
- Bodie, Z., & Crane, D. B. (1997). Personal investing: Advice, theory, and evidence. Financial Analysts Journal, 53(6), 13-23
Noten
- Op basis van het theoretisch beschermingsrendement, waarbij al het overig rendement onderdeel is van het toe te delen overrendement.
- Alserda, G., 2022, Renteafdekking in het nieuwe pensioenstelsel. De Actuaris 30-2
- Wanneer het financieel kapitaal 25% van het totale kapitaal is en de gewenste blootstelling ook 25% is moet dus 100% van het financieel kapitaal in zakelijke waarden worden belegd.
- In de Wet Toekomst Pensioenen is de maximale blootstelling naar overrendement vastgesteld op 150%, hoewel nog niet duidelijk is wat hier allemaal in meetelt.
- Het aantal mogelijke lifecycles is bijna oneindig. Hierdoor is een volledige optimalisatie met behulp van een simulatiemodel niet te doen.
- Om de zekerheidsequivalent te berekenen maken we gebruik van de inverse nutsfunctie. Hier voeren we het verwachte (gemiddelde) nut in dat volgt uit de simulaties van verschillende lifecycles.
in VBA Journaal door Gosse Alserda, Oliver Warren en Gerard Moerman