Association of Investment Professionals in the Netherlands
My membership

Dual-Duration Matching

Back to recent publications

Introduction

Liability-relative investment approaches are described in two major strands of the literature. The more general strand concerns surplus asset allocation, which adapts the mean-variance return-risk balancing notions of Markowitz efficient frontiers to include liabilities as an asset held short. And there is the cash-flow matching and duration-matching strand, exemplified by the many articles on this topic by Leibowitz (1992). I pay primary attention to the latter, but with a couple of new twists. First, I cast duration matching in the context of the more fully general optimization solution, showing it is a special case in the family of surplus optimal approaches. Second, I refine duration matching by decomposing nominal rates into their two principal components, real interest rates and inflation rates, a dual duration approach. Third, I show how to separately measure and manage both of these durations across all asset classes (not just bonds) to better manage the risks of the pension plan. Finally, I propose an integration of the duration-matching solution with the surplus asset allocation solution, for a complete pension risk-management solution.

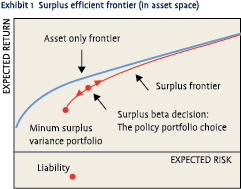The optimization problem in a DB pension plan is to maximize the utility of a portfolio of assets that is constrained to also hold short an asset with the economic or market characteristics of the pension liability. This approach is often called surplus optimization. Exhibit 1 compares an asset-only efficient frontier to a surplus efficient frontier, and shows how the surplus frontier relates to the liability. In a DB plan, the liability measure that is relevant to sound pension management is the economic liability, the best estimate of expected future cash flows (in the statistical sense), discounted back to the present at an appropriate discount rate.

 

Managing assets to pay the liability

Interest rate price sensitivity, or duration, is a risk that can be partly captured by the mean-variance parameters of liability-relative or surplus optimization. But that has more typically been managed through cashflow matching or duration matching. Cash-flow matching dedicates each cash flow in the assets to paying a cash flow in the liability, usually through a laddered structure of nominal bonds. It has received renewed attention lately, to some extent in the US, but mostly in other countries and particularly in the UK. Duration matching (sometimes called immunization) has much in common with cash-flow matching, but is in some ways simpler to implement. Duration matching is accomplished by holding a portfolio of assets with the same duration as the liability (but not necessarily the same timing of cash flows), with the expectation that as interest rates change, both the assets and liabilities will change together.

A portfolio managed using duration matching will consist mostly or entirely of fixed income assets. Should we just come close to minimizing surplus risk through duration or cash-flow matching, and then stop, so that the pension portfolio is a fixed income portfolio? No—the complete decision is where on the surplus efficient frontier we want to be, how aggressive the investments should be. As soon as we move to a more aggressive policy than the minimum surplus variance policy, equities and other asset classes enter the portfolio, asset classes that we haven’t in the past known how to include when we use durationmatching techniques. Viewing the duration-matched portfolio as a proxy for the minimum surplus variance portfolio in Exhibit 1, we can see there is not a dichotomous choice to be made between duration or cashflow matching on the one hand and surplus optimization on the other; instead, there is a continuum.

 

Duration in terms of inflation risk and real interest rate risk

Can we remain duration matched even with equities in the portfolio? Most of the principal issues in duration matching were developed by Leibowitz who, with numerous coauthors, has written many valuable articles on the topic. Our point of departure is “Total portfolio duration” (Leibowitz 1986), which begins to develop the concept of equity duration along the path to measuring the duration of a total multiasset-class portfolio. As most plan sponsors hold some equity, Leibowitz reasons, understanding the duration of equities would be important to the duration matching or asset-liability-management process. Leibowitz et al. (1989) noted that equities don’t have a single, nominal duration as do conventional bonds, but rather two separate durations: one with respect to changes in real interest rates, and another with respect to changes in inflation rates; and that equities have a high real interest rate duration of maybe 20 years or more, and a low inflation duration of around 4 years. The directional conclusion makes intuitive sense—changes in inflation tend to be passed through to customers in the prices of goods and services, so that the real value of the firm and its securities is kept reasonably stable. Changes in the real discount rate, though, substantially change the present value of the firm, as they would for any longterm set of cash flows. Readers who have studied the empirical data relating inflation to equity pricing will know that a very low proportion of equity variance (r-squared) is statistically explained by inflation and real interest rate changes. Many factors other than inflation and real rates strongly affect equity prices, swamping these effects. And in fact my most recent estimates of the dual durations of equities are based on empirical studies and are lower than those of Leibowitz; they are zero for the inflation duration and 8 for the real interest rate duration.

We thus cannot expect precision in estimating the dual durations of equities to predict specific price changes. But if we accept that the dual duration applies to equities in principle, then the price changes are there, and this is a useful tool even if it is imperfectly observable. In fact, the inflation duration and real interest rate duration are different for most financial instruments. Nominal bonds, rather than being the general case, are actually the special case in which inflation rate sensitivity and real interest rate sensitivity are functionally identical. Think through the pricing equations for commodities, real estate and any other real assets. The assets all have different real interest rate and inflation durations. We can use this insight in a comprehensive asset allocation policy process, one that incorporates dual duration matching but that is preferably also founded on surplus optimization.

 

Liabilities

Conventional practice has been to characterize the liability as having a single nominal duration. This also is incomplete, as the literature has been clear for some time. Goodman and Marshall (1988) observed more than 15 years ago that the liability has separate inflation and real interest rate durations. The inflation duration of liabilities is quite low—practically zero for pension plans with full cost-of-living allowances (COLAs), and somewhat higher (but still low) for non-COLA plans. The real interest rate duration of the liability is quite high. These properties make intuitive sense. In a typical plan, where benefits are determined by final pay schemes or average income schemes, the benefit payment streams related to active and future lives are sensitive to wage inflation or price inflation (which I’ll treat both like generalized inflation for this exercise), so that the present values of these payment streams have low and nearzero inflation duration. The intuition that a pension liability has a low inflation duration and a high real interest rate duration is more clear when we separate inflation from the real discount rate in the denominator of the model—and see that much of the inflation cancels out between the numerator and the denominator:

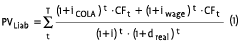
with the first term in the summation reflecting retired lives and the second term reflecting active and future lives.

Once we have estimates for the dual durations of the liability, achieved with the help of the plan’s actuary, we can dual duration match the assets and the liabilities.

 

Implementation: The role of TIPS

With the arrival of US Treasury inflation-protected securities, or TIPS, in 1997, a tool that clearly helps us to adjust the inflation sensitivity of a portfolio became available. UK inflation-indexed bonds, called linkers, were first issued in 1981; Sweden, France, Canada and Japan also have such bonds. Germany will soon have them too. The price of TIPS won’t change with changes in the inflation rate, but the price will change with changes in the real interest rate. Thus the inflation duration of TIPS is zero, while the real interest rate duration of TIPS is numerically similar to that of a nominal bond of the same maturity. A nominal bond, by contrast, has nearly identical real interest rate and inflation durations.

 

Matching dollar dual durations

Duration matching is good shorthand for the practice of protecting an asset-liability portfolio from various kinds of interest rate risk, but it is an incomplete term; simple matched durations protect a portfolio’s value relative to the liability only if the assets are equal to the liability in dollar size. The more appropriate objective is dollar duration matching (see Kahn [1990]). The result of matching the dollar duration of the assets (A • DA) with the dollar duration of the liabilities (L • DL) is that, regardless of the A/L ratio, changes in the dollar value of the liability sourced in real interest rate or inflation changes are offset by equal changes in the dollar value of the asset portfolio. Thus, ideally, we would set the dollar durations of the assets to be equal to that of the liability:

where A is the dollar value of the assets, L is the dollar value of the liabilities, and D is the duration of the subscripted element. Equation (2) must hold for any type of duration. We will make it hold true separately for both inflation and real interest rate durations, introducing a subscript notation that characterizes both the real interest rate duration and the inflation duration (indicated by Dr and Di respectively), and indicating whether a given duration pertains to an asset or liability:

   and    

We can use a more compressed notation to condense Equations (3) and (4) into one expression, using subscript parentheticals to indicate the ordered pairs of real interest rate and inflation durations:

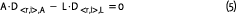
We can restate Equation (5) to reflect a multi-assetclass portfolio, to accommodate the asset classes of most interest to us. These are conventional nominal bonds, inflation-linked bonds (TIPS) and equities:

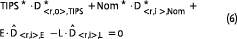
where TIPS, Nom, and E are the dollar values of the TIPS, nominal bond, and equity portfolios respectively, and A = TIPS + Nom + E (the dollar values of the asset classes naturally sum to the total dollar value of the assets). We indicate the unknowns we must solve with asterisks, and the “given” durations of equities and of the liability with a circumflex.

 

Solving the dollar duration matching puzzle

We provide here an algebraic solution to the question. In Equation (7), there are four unknown values: the dollar values and duration of TIPS, and the dollar value and duration of nominal bonds. Despite the many moving parts, the problem can be readily solved if one assumes that the dollar value of the equities (E) is known, meaning that this duration matching process must be undertaken after the overall equity/fixed income asset allocation decision has been completed. If we know E, then we also know what amount (A – E) is left over to be allocated to TIPS or nominal bonds with which we can adjust the duration of the total asset portfolio. Starting with the fact that the inflation duration of TIPS is zero, we can see that the first term of the inflation duration version of Equation (6) is necessarily also zero. With only two nominal terms to deal with, this version is the natural place to start. And if we assume a starting value for one unknown, say, the duration of the nominal bond portfolio D(r=i)Nom (or simply DNom), we can solve Equation (6) directly for the other unknown, the dollar size of the nominal bond portfolio:

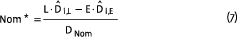
Since the total value of the assets is fixed, and the equity portion is a given, once we have determined the value of the nominal bond portfolio, we have also necessarily determined the value of the TIPS portfolio as the remainder:

We now have three pieces of the four-piece puzzle: the dollar size of the TIPS, the dollar size of the nominal bond portfolio, and the (assumed) duration of the nominal bond portfolio. With those pieces in hand, we can solve the fourth and final piece, using the real interest rate version of Equation (6), to determine the last unknown, the required real interest rate duration of the TIPS portfolio, D r TIPS , * :

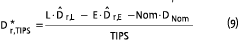
This solution is just one of a family of solutions. For any starting value for nominal bond duration, we get a different and valid solution.

 

Generalization to surplus measures

We can use this machinery to measure the dollar duration of the surplus. We do so by measuring the values of the left hand side of Equation (2) and defining the result as the dollar duration of the surplus:

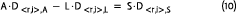
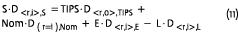
In these equations, I’ve defined the dollar duration of the surplus by multiplying the duration of the surplus by (naturally enough) the dollar value of the surplus itself, indicating this with the subscript S. The most intuitive measure of the duration of the surplus—that is, the return of the surplus conditional on a unit change in the relevant interest rate or interest rate component—would be found by dividing both sides of Equation (11) by the value of the surplus, S. But if S is zero, there is a zero-divide problem, and DS is undefined. For these reasons, I prefer to define the duration of the surplus by scaling not to S but to the dollar size of the liability, L, which has a more stable dollar value than the surplus (and doesn’t go to zero—if it did, we wouldn’t have to worry about duration matching). To differentiate this in notation, we’ll refer to it as D,S(L), read as duration of the surplus scaled to the liability—rather than the more “natural” D,S(L):

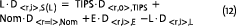
This liability-referenced version of surplus duration is then given by:

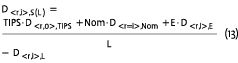
Using this duration-based measure of surplus risk, one can measure and quantify for any pension plan the surplus inflation dollar duration (change in the dollar value of the surplus caused by a single percentage point change in the inflation rate), and the surplus real interest rate dollar duration (change in the dollar value of the surplus caused by a single percentage point change in the real interest rate). In a prototype plan which we modeled using a set of reasonable assumptions, the durations of the surplus, when there are no TIPS and the bonds are all benchmarked to the Lehman Aggregate, are Dr = –4.12 and Di =–0.80. The inflation duration isn’t too problematic in this example, but a four-year real interest rate duration for the surplus is not trivial: it means that for every percentage point decline in real interest rates, there will be a 4.12% decline in the surplus as a percentage of the liability. This is a fair amount of surplus risk in the real rate dimension. The durations of the surplus are thus measures every plan sponsor should know about its plan, on at least an annual basis. If the surplus dollar duration measures indicate that a plan is more exposed to rate risk than is comfortable, the portfolio should be adjusted to reduce that risk to some acceptable target level of surplus dollar durations.

 

The best of both: Combining surplus optimization and duration matching

As we have shown, if the mix of asset classes is on the surplus efficient frontier, with nominal bonds and TIPS considered as a singe asset class, we can find the dual duration-matched portfolio of nominal bonds and TIPS that will zero out the risk related to inflation rate changes and real interest rate changes. Thus we can be both surplus optimal and dollar duration matched at the same time.

As some readers may have intuited, it is possible, at least conceptually, to deal with these risks in the mean variance surplus optimization process itself. Given access to long-term and short-term nominal bonds and TIPS as separate asset classes, the optimizer could choose the mix with the correct durations. But the estimates of the correlation matrix would have to be very accurate for the investor to be confident of the results. (The correlation matrix is one of the sets of inputs on which the optimizer depends, and represents the expected correlation of each asset class with every other asset class, and with the liability.)

If we made the dual-duration matching step explicit, while still using an optimizer, we can be more confident of the outputs. A relatively graceful way to achieve this is to add equations (3) and (4) as linear constraints in the optimization problem. The first constraint requires that the asset portfolio be matched to the liability in dollar inflation duration. The second constraint accomplishes the same goal for dollar real interest rate duration. The end result is a portfolio that is both dual-duration matched and mean-variance optimal.

 

Conclusion

Surplus optimization, with its ability to balance both return expectations and risk expectations, should be the dominant pension investment policy tool. But controlling surplus duration, in both inflation and real interest rate dimensions, adds a useful and important additional level of risk control to the plan. The sponsor gains the benefits of dual duration risk control even while continuing to hold some amount of equity in the policy mix, an amount determined by a sensible, liability-relative, surplus efficient frontier. There is no need to consider the extreme positions of cash-flow matching or duration matching in an all-bond context, as has been typical.

Duration-matching results aren’t perfectly visible in the presence of equities. Even so, the opportunity to gain greater control over risk by integrating these approaches in the policy development process is substantial and additive, and not to be missed. These tools for calculating the ideal real interest rate and inflation durations let us quantify and control just how much duration mismatch an organization may want to incur. They are useful and informative, and investors funding a liability should employ them.

 

References

Notes

  1. This article is based on Waring, M. Barton, “Liability-Relative Investing” and “Liability-Relative Investing II,” in, respectively, the Summer 2004 and Fall 2004 issues of The Journal of Portfolio Management. The article was edited by Laurence Siegel, Director of Research at the Ford Foundation, New York and Helmut Cardon, Investment Strategist at the Shell Pension Fund.

 

in VBA Journaal door

Download
Subscribe to our newsletter
© 2024 CFA Society Netherlands. All rights reserved.
Maatwerk website door Omines Internetbureau