Keuze berekening beschermingsrendement bepaalt invulling collectieve portefeuille

Pensioenfondsen die kiezen voor de solidaire premieregeling – voorheen bekend als het nieuwe pensioencontract – moeten vervolgens een keuze maken tussen twee methodes om het beschermingsrendement vast te stellen. De keuze gaat hier tussen een theoretisch beschermingsrendement gebaseerd op de DNB swapcurve of een werkelijk beschermingsrendement gebaseerd op het rendement van één of meerdere matchingportefeuilles. Beide methodes hebben specifieke voor- en nadelen, en leiden naar verwachting ook tot een andere invulling van de collectieve portefeuille. Om een goede keuze te maken tussen de twee methodes is het daarom belangrijk om eerst te bepalen hoe de collectieve portefeuille eruit komt te zien bij elk van deze methodes.

In dit artikel volgen we twee deelnemers – Jan en Laura – en bekijken we de impact van de keuze van het type beschermingsrendement op hun pensioenresultaat. We gaan eerst in op de werking van beide methodes. Vervolgens stellen we voor beide methodes vast hoe – naar onze mening – het beschermingsrendement kan worden ingevuld. Ten slotte vergelijken we beide methodes en presenteren de voor- en nadelen van beide, die afhankelijk zijn van de voorkeuren van een pensioenfonds.

DE THEORETISCHE METHODE UITGELEGD

Wanneer een pensioenfonds gebruik maakt van de theoretische methode om het beschermingsrendement vast te stellen dan krijgt elke deelnemer een beschermingsrendement bijgeschreven dat gelijk is aan de vastgestelde renteafdekking vermenigvuldigd met de verandering van de kostprijs van het pensioen op basis van de DNB swapcurve, oftewel de prijs van een (uitgestelde) annuïteit. Voor het gedeelte dat niet is afgedekt (1 – renteafdekking) wordt het kasrendement (de 1-jaars swaprente) bijgeschreven.

Beschermingsrendement = renteafdekking x ∆kostprijs pensioen + (1 – renteafdekking) x kasrendement

Dit betekent dat het beschermingsrendement onafhankelijk is van het rendement op de feitelijke beleggingen. Het beschermingsrendement wordt afgetrokken van het totaal rendement en wat overblijft is het overrendement. Hierbij wordt enkel gekeken naar de nominale renteafdekking: inflatiebescherming in het beschermingsrendement is onder deze methode niet mogelijk.

DE WERKELIJKE METHODE UITGELEGD

Het beschermingsrendement bij de werkelijke methode is gebaseerd op één, of meerdere, aparte matchingportefeuilles. Deelnemers krijgen afhankelijk van hun leeftijd blootstelling aan deze matchingportefeuilles waardoor de renteafdekking op het beoogde niveau komt. Wanneer een pensioenfonds gebruik maakt van deze methode is er dus sprake van een schot tussen de overrendementsportefeuille en de matchingportefeuille(s).

Voor een voorbeelddeelnemer kan het toegedeelde totaalrendement neerkomen op de optelling van het rendement op de overrendementsportefeuille (bijvoorbeeld 50%), matchingportefeuille 1 (bijvoorbeeld 30%) en matchingportefeuille 2 (bijvoorbeeld 20%).

Bij het voorgaande voorbeeld vallen al een aantal punten op:

Een blootstelling van meer dan 100% naar de overrendementsportefeuille lijkt niet mogelijk.1 Leverage is alleen mogelijk binnen de portefeuille (bijvoorbeeld via derivaten);
Ook binnen de matchingportefeuilles is waarschijnlijk leverage nodig om de renteafdekking op het gewenste niveau te krijgen.

De opzet van de solidaire premieregeling mét de werkelijke methode voor het beschermingsrendement is vergelijkbaar met de opzet van de flexibele premieregeling. Er zijn echter ook wel verschillen: De portefeuilles hoeven niet in een fondsstructuur geplaatst te worden, wat vaak wel nodig is in de flexibele premieregeling. Bovendien is de verdeling binnen de overrendementsportefeuille voor alle leeftijdscohorten gelijk, wat niet het geval hoeft te zijn voor de flexibele premieregeling.

Een voordeel van de werkelijke methode is dat er binnen de matchingportefeuilles ook inflatie-gerelateerde beleggingen kunnen worden toegevoegd. Hierdoor kan voor ouderen inflatiebescherming worden ingeregeld.

AANNAMES ANALYSE

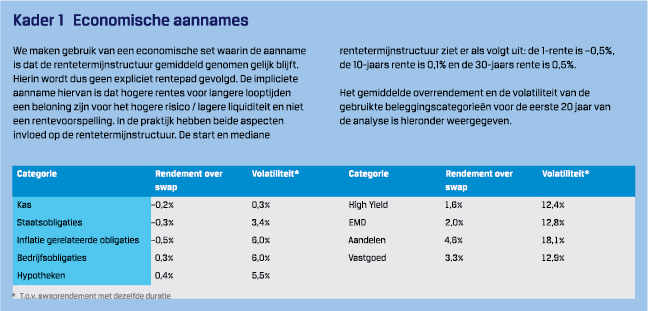
Om de invulling van de beschermingsportefeuille te analyseren maken we gebruik van een scenario-analyse. Hierbij analyseren we het pensioenresultaat voor de twee methodes voor de berekening van het beschermingsrendement en met verschillende invullingen van de portefeuille daarvan. Voor elke invulling analyseren we 2.000 scenario’s over de volledige horizon van de deelnemers. De aannames van de scenario-analyse zijn opgenomen in kader 1.

In de analyse kijken we steeds naar twee deelnemers:

Laura, 25 jaar oud en net begonnen aan haar eerste baan met een salaris van €25.000
Jan, 60 jaar oud en al zijn hele leven deelnemer bij het pensioenfonds. Zijn huidige salaris is €50.000 en hij heeft €250.000 aan pensioenkapitaal opgebouwd.

We nemen aan dat het salaris van zowel Laura als Jan zich ontwikkelt met de looninflatie en een leeftijdsafhankelijke carrièrestijging. Er wordt een vlakke premie ingelegd van 20% over het pensioengevend salaris en de toedelingsfactoren volgen de volgende impliciete lifecycle2:

Renteafdekking: 25% tot leeftijd 25 en dan lineair opbouwend naar 75% op pensioenleeftijd
Overrendement: 150% tot leeftijd 25 en dan lineair afbouwend naar 35% op pensioenleeftijd

De overrendementsportefeuille bestaat – tenzij anders aangegeven – uit de volgende portefeuille: bedrijfsobligaties (10%), hypotheken (15%), High Yield (7,5%), EMD (7,5%), wereldwijde aandelen (50%) en beursgenoteerd vastgoed (10%). Renteafdekking wordt zoveel mogelijk onttrokken uit de fysieke portefeuille (inclusief overrendementsportefeuille) en aangevuld met renteswaps.

Als we de toedeling naar overrendement – gewogen naar kapitaal - voor alle deelnemers in het pensioenfonds optellen komen we uit op een collectief gewicht naar overrendement van circa 50% van het totaal vermogen. Om complexiteit te reduceren houden we deze verhouding constant, terwijl deze in de praktijk (in beperkte mate) zal variëren met onder andere marktbewegingen. De impact hiervan is naar onze verwachting beperkt.

INVULLING VAN DE PORTEFEUILLE ONDER DE THEORETISCHE METHODE

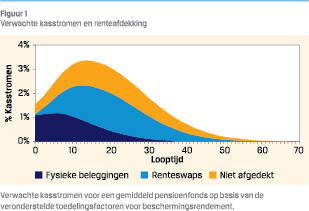
Wanneer gekozen wordt voor de theoretische methode is de invulling van de renteafdekking relatief eenvoudig. Als eerste moet worden vastgesteld hoeveel rente er voor elk leeftijdscohort wordt afgedekt; dit is onderdeel van de impliciete lifecycle. Op basis hiervan kan een af te dekken kasstromenprofiel worden berekend, dat de optelling is van verwachte pensioenuitkeringen keer de gewenste renteafdekking voor elk leeftijdscohort. Dit kasstromenprofiel is vergelijkbaar met wat we nu al kennen in uitkeringsregelingen (Financieel Toetsingskader; FTK). De afdekking van de kasstromen wordt als eerste gevuld vanuit beleggingen die vanuit het overrendement zijn opgenomen maar wel bijdragen aan de renteafdekking, zoals bedrijfsobligaties en hypotheken. De resterende af te dekken kasstromen worden – in beginsel – afgedekt door middel van renteswaps, die de sterkste samenhang hebben met het toe te delen beschermingsrendement. Figuur 1 laat zien hoe dit er in de praktijk uit kan zien. Hierbij bestaat het gele gebied uit niet afgedekte kasstromen, het donkerblauwe gebied uit de afdekking vanuit fysieke beleggingen en het restant – het lichtblauwe gebied – uit afdekking vanuit renteswaps.

Voor de invulling van de renteafdekking betekent dit concreet dat er renteswaps gebruikt worden tenzij het overrendement – rendement minus rendement op renteswap met hetzelfde kasstromenprofiel – van een andere rentegevoelige belegging interessant is vanuit een overrendementsperspectief. Oftewel, als men bedrijfsobligaties toevoegt aan de portefeuille zal hierdoor minder in renteswaps belegd worden. Dit is alleen interessant als het overrendement van bedrijfsobligaties de risico-/rendementsverhouding van het overrendement verbetert.

De opzet van de renteafdekking met een collectieve portefeuille waarbij de rentegevoeligheid van beleggingen wordt toegeschreven aan de renteafdekking en het restant overblijft voor het overrendement is sterk vergelijkbaar met huidige uitkeringsregelingen, waar de resterende renteafdekking vaak ook met renteswaps wordt ingevuld.

OPZET RENTEAFDEKKING VERANDERT NIET STERK BIJ KEUZE VOOR THEORETISCHE METHODE

Voor de theoretische methode analyseren we drie varianten, die zijn weergegeven in tabel 1. Voor elke variant is de invulling van het overrendement hetzelfde: het verschil zit hier dus in de rest van de portefeuille wat we voor de eenvoud de beschermingsportefeuille noemen.

VARIANT 1: KAS EN SWAPS

Het uitgangspunt bij de theoretische methode is een collectieve portefeuille die bestaat uit enerzijds de overrendement beleggingen en anderzijds kas aangevuld met renteswaps om tot de gewenste renteafdekking te komen. Dit sluit in theorie precies aan bij de verdelingsregels in de solidaire premieregeling, waardoor er geen ruis vanuit de renteafdekking bij het overrendement terecht komt. Hoewel er in de praktijk wel sprake zal zijn van enige mate van ruis – bijvoorbeeld omdat een perfecte afdekking over alle kasstromen veelal niet mogelijk is en/of omdat het rendement op fysieke kas afwijkt van de 1-jaars swaprente3 – leidt deze variant wel tot het minste ruis en is daarom een goede neutrale uitgangsituatie. De resultaten voor Laura en Jan van deze variant zijn weergegeven in tabel 2 en vormen de basis om de andere varianten te vergelijken.

VARIANT 2: STAATSOBLIGATIES

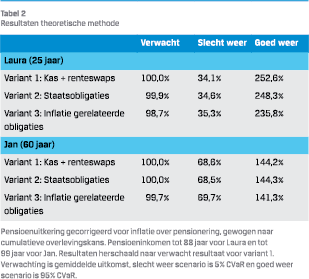Hoewel variant 1 het beste aansluit bij de berekeningsmethode van het beschermingsrendement, zorgt het wel voor een zeer grote positie in kas, in ons voorbeeldfonds wel 50% van het totaal vermogen. Vanuit risicoperspectief is dat vaak ongewenst, omdat een fysieke belegging in kas – bijvoorbeeld een rekening bij een bank of een belegging in een geldmarktfonds – in veel gevallen toch kredietrisico kent en de grote positie leidt tot concentratierisico. Daarom zullen de meeste pensioenfondsen kiezen om (gedeeltelijk) in staatsobligaties te beleggen in plaats van kas. Uiteraard geldt ook in dit geval dat de rentegevoeligheid van de toegevoegde staatsobligaties wordt gecompenseerd door minder blootstelling naar renteswaps. Omdat de rente op staatsobligaties normaal gesproken lager is dan op renteswaps (als gevolg van de swapspread) blijft het rendement achter bij het veronderstelde beschermingsrendement: dit komt bij de theoretische methode terecht bij het overrendement. Dit is echter vergelijkbaar met variant 1, waar sprake is van een verschil tussen het daadwerkelijk kasrendement en de 1-jaars swaprente die gebruikt wordt om beschermingsrendement vast te stellen. Zoals in tabel 2 te zien valt zijn de resultaten voor zowel Jan als Laura dan ook sterk vergelijkbaar. Enkel voor Laura verbetert het slecht weer scenario enigszins, dit is een gevolg van het feit dat de swapspread normaal gesproken stijgt tijdens neergaande markten.

VARIANT 3: INFLATIE GERELATEERDE OBLIGATIES

Wanneer oplopende inflatie als een belangrijk risico wordt gezien kan men overwegen om inflatie gerelateerde obligaties toe te voegen aan de beschermingsportefeuille. In variant 3 hebben we daarom 50% inflatie gerelateerde staatsobligaties aan de beschermingsportefeuille toegevoegd. Binnen de theoretische methode wordt echter alles dat afwijkt van de nominale renteafdekking toegedeeld aan het overrendement, zo ook de inflatiebescherming. De inflatiebescherming komt dus voornamelijk bij jongeren terecht, terwijl ouderen – vanwege de kortere horizon – de bescherming het meest nodig hebben. De resultaten in de tabel laten zien dat zowel voor Laura als voor Jan het neerwaarts risico afneemt als gevolg van de inflatiebescherming. Dit gaat echter wel ten koste van het verwacht pensioenresultaat, dat vooral voor Laura fors daalt. Dit is een gevolg van de inflatierisicopremie, waardoor nominale obligaties normaal gesproken een hoger verwacht rendement hebben dan vergelijkbare inflatie gerelateerde obligaties.

SUBCONCLUSIE THEORETISCHE METHODE

We verwachten dat voor de meeste pensioenfondsen variant 1 afvalt, omdat de blootstelling naar kas in dat geval te veel kredietrisico oplevert. Er zal binnen de theoretische methode dus nog steeds substantieel belegd worden in staatsobligaties. Pensioenfondsen met een sterk reële doelstelling kunnen overwegen om hiervoor inflatie gerelateerde obligaties in te zetten, hierdoor neemt het neerwaarts (reële) risico af, ten koste van het verwacht pensioenresultaat. Echter binnen de theoretische methode komt de inflatiebescherming vooral bij jongeren terecht, die er vanwege hun lange horizon vaak minder belang bij hebben. De werkelijke methode biedt meer mogelijkheden om inflatiebescherming voor ouderen in te richten.

STAATSOBLIGATIES BLIJVEN OOK BINNEN DE SOLIDAIRE PREMIEREGELING VAN BELANG

Voor de theoretische methode hebben we niet gekeken naar varianten waarbij meer risicovolle beleggingen (bijvoorbeeld bedrijfsobligaties) worden toegevoegd aan de beschermingsportefeuille. Vanwege de opzet van deze methode is er geen sprake van een schot tussen de overrendement- en de beschermingsportefeuille, zodat ongeacht waar deze beleggingen worden geplaatst, het risico altijd bij het overrendement terecht komt. Wanneer dit soort beleggingen in de beschermingsportefeuille geplaatst worden is de impact op het overrendement afhankelijk van de omvang van de beschermingsportefeuille ten opzichte van de overrendementsportefeuille. Als de overrendementsportefeuille relatief klein is dan heeft een beperkte afwijking in het beschermingsrendement mogelijk al een grote impact op het overrendement.

INVULLING VAN DE PORTEFEUILLE ONDER DE WERKELIJKE METHODE

De portefeuille onder de werkelijke methode bestaat uit een overrendementsportefeuille en een of meerdere matching portefeuilles. Voor deze analyse gaan we uit van vier matching portefeuilles. Deze zijn als volgt opgebouwd:

Maximale duratie; Portefeuille met een duratie van 100 jaar,4 hierdoor wordt met minimaal gewicht zoveel mogelijk renteafdekking verkregen. Dit is vooral voor jongeren relevant. Vanwege de hoge duratie is enkel een invulling met kas en swaps mogelijk.
Hoge duratie en spread; Portefeuille met een duratie van 20 jaar en beleggingen in hypotheken, bedrijfsobligaties, kas en renteswaps.
Lagere duratie en spread; Vergelijkbaar aan matching portefeuille 2, maar dan met een duratie van 10 jaar
Kas; Belegging in kas en korte staatsobligaties met een zeer korte duratie. Vanwege de korte duratie en voornaamste inzet voor ouderen wordt niet belegd in spreadproducten.

LEVERAGE BINNEN DE WERKELIJKE METHODE ALLEEN MOGELIJK MET DERIVATEN, WAT LEIDT TOT MEER COMPLEXITEIT EN KOSTEN

Gezamenlijk kunnen deze vier matching portefeuilles worden ingevuld om voor ieder leeftijdscohort de gewenste mate van renteafdekking op te bouwen met een zo goed mogelijke afdekking over de curve.5 Daarnaast zorgt het – in de basisvariant – voor een vergelijkbare collectieve portefeuille als in de basisvariant voor de theoretische methode. Dit vereenvoudigt de vergelijking tussen beide methodes. De vier varianten die we analyseren zijn samengevat in tabel 3.

VARIANT 1: MET LEVERAGE

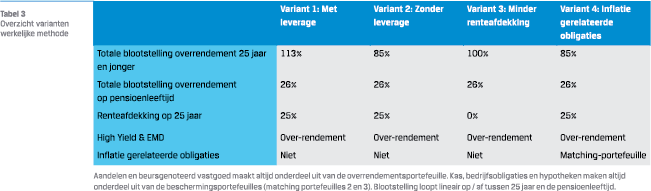Variant 1 is zo opgezet dat deze zoveel mogelijk vergelijkbaar is met variant 1 van de theoretische methode. Om de benodigde leverage te krijgen van het overrendement wordt er binnen de overrendementsportefeuille met leverage belegd. Dit kan bijvoorbeeld door gebruik te maken van futures. De leverage6 bedraagt 150%, terwijl bedrijfsobligaties en hypotheken buiten het overrendement zijn geplaatst. Zo is de blootstelling aan de overige overrendement categorieën precies hetzelfde als bij de theoretische methode. Bedrijfsobligaties (7,6%) en hypotheken (11,4%) zijn in matchingportefeuilles 2 en 3 geplaatst, waarbij het gewicht zo is gekozen dat het op collectief niveau hetzelfde is als bij de theoretische methode.

Uit de resultaten blijkt dat dit voor jongeren zoals Laura leidt tot een beperkt beter pensioenresultaat. Voor ouderen zoals Jan is er vrijwel geen verschil met de basisvariant van de theoretische methode. De basisvariant leidt dus tot vergelijkbare of beperkt betere resultaten dan de basisvariant in de theoretische methode. De complexiteit is echter een stuk hoger, waarbij gebruik gemaakt moet worden van derivaten om de benodigde leverage te verkrijgen. Dit leidt onder andere tot hogere kosten (in deze analyse niet meegenomen). We verwachten dat deze variant daarom voor veel pensioenfondsen afvalt.

VARIANT 2: ZONDER LEVERAGE

Voor de tweede variant hebben we de gewichten in de overrendementsportefeuille zo teruggeschaald dat er geen leverage meer nodig is. Dit houdt in dat de effectieve blootstelling aan overrendement lager is voor leeftijden tot en met 41 jaar. Deze variant is voor de meeste pensioenfondsen realistischer dan variant 1.

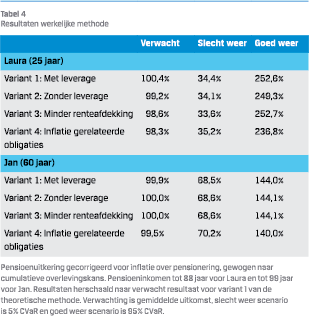
Tabel 4 laat zien dat hierdoor het pensioenresultaat voor Laura sterk afneemt. Zowel de verwachting als het slecht weer scenario wordt minder door een lagere blootstelling aan overrendement en een minder goede spreiding van risico over tijd. De beleggingsmix voor Jan blijft vrijwel gelijk en daardoor is de impact op zijn pensioenresultaat zeer beperkt.

VARIANT 3: MINDER RENTEAFDEKKING

In variant 3 passen we geen leverage toe in het overrendement, maar houden we het risiconiveau zoveel mogelijk op peil door de renteafdekking in de eerste jaren weg te laten en het kapitaal dat beschikbaar komt te alloceren naar het overrendement. Verder is deze variant gelijk aan variant 2.

Ten opzichte van de voorgaande twee varianten zorgt dit in onze analyse voor minder goede resultaten. Het is voor Laura dus belangrijker om de renteafdekking in stand te houden dan om de blootstelling naar overrendement te maximeren. Dit komt onder andere door het diversificatievoordeel van de renteafdekking in combinatie met het overrendement. Voor Jan is er geen verschil met variant 2 omdat de blootstelling op latere leeftijd gelijk is.

VARIANT 4: INFLATIE GERELATEERDE OBLIGATIES

Ten slotte voegen we in variant 4 inflatie gerelateerde obligaties toe aan de matching portefeuilles 2 en 3. Net als bij variant 3 van de theoretische methode gaat dit door de inflatierisicopremie ten koste van het verwacht pensioenresultaat en het pensioenresultaat in het goed weer scenario. Echter, we zien dat het slecht weer scenario sterk verbetert, met name voor Jan. In tegenstelling tot de theoretische methode komt de inflatiebescherming hier namelijk terecht bij ouderen, waardoor zij er meer voordeel van hebben. Voor jongeren is vanwege de lange horizon enerzijds het effect van de inflatierisicopremie groter en is anderzijds de impact op het risico relatief kleiner omdat andere risico’s domineren. Het is belangrijk om te beseffen dat jaarlijkse veranderingen tijdens pensionering niet per se kleiner worden bij deze variant. De waarde van inflatie gerelateerde obligaties bewegen namelijk mee met veranderingen in de verwachte inflatie, wat iets anders is dan de actuele inflatie. Bij een structureel lagere inflatie neemt daardoor bijvoorbeeld de waarde van de beleggingen veel sterker af dan alleen de lagere inflatie in dat jaar zelf. Hierdoor neemt de volatiliteit van het reëel pensioen op de korte termijn mogelijk juist toe. Het spreiden van schokken over tijd zou hiervoor in zekere mate een oplossing kunnen bieden.

SUBCONCLUSIE WERKELIJKE METHODE

Als we kijken naar de vier varianten die we hebben doorgerekend voor de werkelijke variant, dan valt op dat over het algemeen de eerste variant de beste resultaten geeft voor Jan en Laura. We verwachten niet dat veel pensioenfondsen voor deze variant gaan kiezen. Het direct toepassen van leverage binnen een portefeuille – anders dan impliciet bij de theoretische methode – zorgt namelijk voor veel complexiteit en hoge kosten. Het is daarom waarschijnlijk dat een van de andere varianten de voorkeur zal krijgen binnen deze methode. Van de overige varianten lijkt – op basis van onze aannames – variant 2 dan de beste resultaten te geven. Hierbij wordt de blootstelling naar overrendement verlaagd, zodat er geen sprake is van leverage binnen het overrendement en ook de renteafdekking in stand kan blijven. Variant 4 zorgt voor de laagste risico’s van het reëel pensioen en biedt met name meerwaarde voor pensioenfondsen die graag directe inflatiebescherming willen bieden.

BINNEN DE WERKELIJKE METHODE IS EEN BETERE INFLATIEBESCHERMING MOGELIJK

Het is interessant te zien dat de vier varianten die we doorgerekend hebben allemaal in theorie ook gerepliceerd kunnen worden binnen de flexibele premieregeling, hoewel het in dat geval nodig kan zijn dat portefeuilles worden omgezet in (gecombineerde) beleggingsfondsen. Pensioenfondsen die een voorkeur hebben voor het beschermingsrendement op basis van werkelijk rendement doen er daarom goed aan om na te gaan of de flexibele premieregeling niet hetzelfde en mogelijk meer kan bieden.

CONCLUSIE

In dit artikel hebben we de theoretische en de werkelijke methodes voor het beschermingsrendement geanalyseerd. Hieruit komt naar voren dat de keuze tussen deze twee methodes naar verwachting impact heeft op de invulling van de beleggingsportefeuille.

De theoretische methode biedt vooral meerwaarde doordat het leverage van het overrendement mogelijk maakt zonder dat hiervoor derivaten gebruikt hoeven te worden. Zodoende wordt er optimaal gebruik gemaakt van het collectief kapitaal, waardoor complexiteit en kosten lager zullen zijn dan bij leverage met behulp van derivaten. Op basis van onze aannames zien we dat het toepassen van leverage voor jongeren meerwaarde biedt in termen van pensioenresultaat en daarmee een voorkeur geeft voor de theoretische methode. Een ander voordeel van de theoretische methode is dat het een perfecte afdekking over de curve biedt: dit is in de praktijk niet haalbaar bij de werkelijke methode. De meerwaarde hiervan is afhankelijk van hoeveel matching portefeuilles er worden opgezet binnen de werkelijke methode, en dus hoe precies de afdekking daarbinnen kan worden ingericht. De verschillende varianten binnen de theoretische methode geven beperkte verschillen: de invulling van de (impliciete) beschermingsportefeuille is daarom vooral een kwestie van goed risico management.

De varianten van de werkelijke methode geven in onze analyse vooral voor jongeren wat minder goede resultaten wanneer er geen gebruik gemaakt wordt van derivaten in het overrendement. Een groot voordeel van de werkelijke methode is echter dat inflatiebescherming specifiek bij ouderen ingezet kan worden, wat de effectiviteit daarvan vergroot. In de huidige opzet is echter de inflatiebescherming ook binnen de werkelijke methode verre van perfect, zodat er van een goede jaar-op-jaar inflatiebescherming geen sprake is. De werkelijke methode – inclusief de mogelijkheden voor inflatiebescherming – lijkt voor een groot gedeelte te repliceren met de flexibele premieregeling: het is dus de vraag hoeveel meerwaarde deze methode daarom in de praktijk biedt ten opzichte van beschikbare alternatieven.

Noten

Ook indien het wel mogelijk is via interne verrekening tussen portefeuilles dan lijkt dit niet gewenst, omdat het juist de bedoeling van deze methode is om alleen te werken met werkelijke rendementen en geen fictieve rendementen tussen portefeuilles.
Grofweg gebaseerd op de eerste doorrekeningen van het Centraal Plan Bureau: https://www.cpb.nl/sites/default/files/ omnidownload/CPB-Notitie-juni2020-Nieuwe-pensioenregels. pdf
Doordat de rente die op een fysieke kas belegging gehaald wordt veelal lager is dan de 1-jaars swaprente is er sprake van een (ex-ante) herverdeling van het overrendement naar het beschermingsrendement en dus normaal van jongeren naar ouderen. Een vergelijkbaar effect treed op wanneer het beschermingsrendement berekend wordt op basis van de rente o.b.v. UFR. Dit laatste punt hebben we in dit artikel niet meegenomen.
Uitgaande van een initial margin verplichting van 50 x DV01 zou in theorie een duratie van ca. 200 jaar mogelijk moeten zijn. In dit geval moet echter wel bij elke rentestijging kas verkregen worden uit de rest van de portefeuille, wat praktisch niet werkbaar is. Een duratie van 100 jaar kan enige rentevariatie aan, maar leidt nog steeds tot frequente herbalanceringen met de rest van de portefeuille.
In onze analyse gaan we uit van een perfecte afdekking over de curve. In de praktijk zal – vooral met de werkelijke methode – een perfecte afdekking over de curve niet mogelijk zijn omdat er veelal te weinig bouwstenen zijn om elke kasstroom precies af te dekken. Hierdoor ontstaat curverisico. Als de matching portefeuilles goed ingericht worden zal de impact hiervan beperkt zijn. Hoe meer matching portefeuilles er worden opgezet, hoe beter het curverisico beperkt kan worden.
Bijvoorbeeld leverage van aandelen met behulp van futures en de rest fysiek belegd.

15 December 2021 in VBA Journaal door Gosse Alserda en Karin Roeloffs