Rendementsportefeuille in nieuw pensioenstelsel: “One size fits all?”

INLEIDING

Nederland staat aan de vooravond van een ingrijpende verbouwing van het Pensioenstelsel. Werkgevers, werknemers en pensioenuitvoerders hebben tot 1 januari 2027 de tijd om de huidige pensioenregelingen aan te passen naar het nieuwe stelsel. Daarbij moeten zij een keuze maken tussen de solidaire of flexibele premieregeling. Voor beide regelingen staat de life-cycle theorie aan de basis van de vormgeving van de beleggingsportefeuille.

Wij willen in dit artikel bijdragen aan het vraagstuk van de optimale inrichting van de rendementsportefeuille met behulp van een theoretisch raamwerk. Om dit vraagstuk uit te werken baseren we ons op het baanbrekend werk van Markowitz (1952) en Merton (1973) dat in dit artikel vertaald wordt naar een Asset Liability Management context. Er zijn in principe twee mogelijkheden om een rendementsportefeuille te construeren, te weten leeftijdsafhankelijk of gestandaardiseerd (“one size fits all”). Met leeftijdsafhankelijk bedoelen we een ‘automatische’ afbouw van het beleggingsrisico van de rendementsportefeuille naarmate de leeftijd van een deelnemer toeneemt. Dit gebeurt reeds bij de beschermingsportefeuille, waar het renterisico geleidelijk wordt afgebouwd door verhoging van de rentehedge.

Dit artikel bevat zes delen. In het eerste deel leggen we de theorie van het life-cycle beleggen uit in de context van het nieuwe pensioenstelsel. De kwantitatieve toetsing van de optimale samenstelling van de rendementsportefeuille beschrijven wij in de daaropvolgende twee delen. In deel vier maken we een kwalitatieve vergelijking tussen een gestandaardiseerde en een leeftijdsafhankelijke rendementsportefeuille. Maatschappelijk verantwoord beleggen (ESG) vormt een integraal onderdeel van het beleggingsbeleid van de meeste Nederlandse pensioenfondsen en dus ook van de rendementsportefeuille. In deel vijf breiden we het eerder gepresenteerde twee fondsen separatie theorema uit met ESG en delen we de uitkomsten van deze toevoeging voor de optimale samenstelling van de rendementsportefeuille. We eindigen dit artikel met suggesties voor vervolgonderzoek en conclusies. Om alvast een tipje van de sluier op te lichten: onze belangrijkste conclusie is dat een gestandaardiseerde rendementsportefeuille voor alle leeftijdscohorten de beste resultaten geeft.

 

LIFE-CYCLE THEORIE VAN TOEPASSING OP PENSIOENBELEGGEN

PENSIOENBELEGGEN Het nieuwe pensioenstelsel blijft bij zowel de solidaire als de flexibele premieregeling een kapitaalgedekt systeem. Dit betekent dat de ontwikkeling van de rente een belangrijke risicofactor blijft voor de hoogte en stabiliteit van de toekomstige pensioenuitkeringen. In het huidige pensioenstelsel wordt het renterisico collectief afgedekt met laag- of niet-risicodragende instrumenten, zoals renteswaps en zeer kredietwaardige staatsobligaties. Dit gebeurt doorgaans in een beschermingsportefeuille, in het huidige stelsel meestal aangeduid als de matchingportefeuille. Het doel van die portefeuille is het afdekken van het renterisico van de pensioenverplichtingen. De risicovolle beleggingen zijn ondergebracht in de zogenaamde rendementsportefeuille. De doelstelling van deze portefeuille is het behalen van een rendement dat hoger is dan het beschermingsrendement, oftewel het overrendement. Het onderscheid tussen de beschermings- en rendementsportefeuille is eveneens toepasbaar in het nieuwe pensioenstelsel, omdat het renterisico relevant blijft.

In het nieuwe pensioenstelsel krijgen deelnemers een persoonlijk pensioenpotje dat belegd wordt conform de beginselen van de life-cycle theorie. Daarbij is het uitgangspunt dat een deelnemer in het begin van een loopbaan meer beleggingsrisico kan nemen omdat het verdienvermogen van arbeid nog hoog is. Naarmate de carrière vordert neemt de contante waarde van het toekomstig arbeidsinkomen af en wordt het beleggingsrisico van het opgebouwde pensioenvermogen afgeschaald. Met het oplopen van de leeftijd van de deelnemer wijzigt het rendement en risicoprofiel van het persoonlijk pensioenvermogen. De bijdrage van Pistorius in het VBA Journaal van winter 2021 gaat dieper in op deze relatie. Het nieuwe pensioenstelsel weerspiegelt grotendeels de gedachtegang van deze theorie.

Een eenvoudige manier om het rendement- en risicoprofiel van een persoonlijk pensioenvermogen van een deelnemer door middel van de life-cycle theorie te wijzigen, is te variëren in de allocatie tussen de beschermings- en rendementsportefeuille. Dit is al de praktijk in het beheer van het individueel pensioenvermogen door middel van Target Date Funds (Dhillon, 2016). Vanwege onder meer de grote marktomvang van individuele premieregelingen in met name de Verenigde Staten is er relatief veel academisch onderzoek gedaan naar het reduceren van de portefeuillevolatiliteit (bijvoorbeeld Dempster (2016)) en het dynamisch alloceren tussen de twee portefeuilles op basis van wijzigingen in de risicopremies (Arnott, 2013). Beduidend minder onderzoek is beschikbaar naar de optimale samenstelling van de rendementsportefeuille.

Nieuw in het nieuwe pensioenstelsel is de plaats die risicohouding van de deelnemer inneemt. Door middel van risicopreferentie-onderzoek moeten pensioenfondsen de risicohouding van deelnemers per leeftijdscohort in kaart brengen. De risicohouding is bepalend voor de mate van afdekking van het renterisico, het nemen van beleggingsrisico in de vorm van allocatie naar en binnen de rendementsportefeuille en met welk tempo beide risico’s in de tijd worden afgebouwd. Het renterisico is relatief eenvoudig aan te passen door het verhogen of verlagen van de renteafdekking. Daarbij verschilt het renterisico per leeftijdsgroep. Hoe ouder de deelnemer is, des te lager is de rentegevoeligheid van de verwachte pensioenuitkeringen en daarmee het renterisico. Voor een efficiënte beheersing van het renterisico is het raadzaam om de beschermingsportefeuille op maat te construeren en af te stemmen op de rentegevoeligheid van de verwachte pensioenuitkeringen.

Het beleggingsrisico heeft vooral betrekking op de rendementsportefeuille. Naarmate de pensioenleeftijd van een deelnemer nadert, kan het rendement- en risicoprofiel van de beleggingsportefeuille als geheel worden verlaagd door de allocatie naar de returnportefeuille te verlagen. Een andere mogelijkheid is om binnen de rendementsportefeuille te schuiven, bijvoorbeeld door de aandelenallocatie te verlagen ten gunste van minder risicodragende beleggingen. Wat is doelmatiger?

 

GESTANDAARDISEERD OF LEEFTIJDSAFHANKELIJK RENDEMENTSPORTEFEUILLE

Voor de toetsing of de optimale samenstelling van de rendementsportefeuille leeftijdsafhankelijk is, maken we gebruik van een drietal fictieve deelnemers: een starter, een professional halverwege zijn carrière en een gepensioneerde. Onder optimaal verstaan we een portefeuille met het hoogste rendement gecorrigeerd voor risico. Voor iedere deelnemer wordt een rendementsportefeuille geconstrueerd die het overrendement gecorrigeerd voor het risico van de portefeuille ten opzichte van de verwachte uitkeringen maximaliseert:

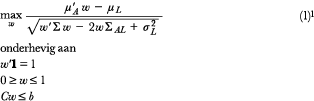
Hierbij is de kolomvector μA het verwachte rendement op de n beleggingscategorieën van de rendementsportefeuille en μL is het verwachte rendement op de verwachte uitkeringen van deelnemer L (starter, professional, of een gepensioneerde). Σ is de covariantiematrix van de beleggingscategorieën, ΣAL de covarianties tussen de beleggingscategorieën en de verwachte uitkeringen, en σ2 L de variantie van de verwachte uitkeringen. De term, Cw ≤ b, is een generieke lineaire inequivalentie restrictie om de wegingen w naar bepaalde beleggingscategorieën te beperken. In onze analyse maximeren we de allocatie naar illiquide beleggingscategorieën, reële activa, op één derde. Dit aandeel is overeenkomstig met de gemiddelde allocatie naar illiquide beleggingen van Nederlandse pensioenfondsen in de rendementsportefeuille.2 Naast de constructie van de rendementsportefeuille die rekening houdt met verwachte uitkeringen wordt ook een portefeuille samengesteld die gemaximaliseerd is ten opzichte van (risicovrij) kasgeld met dezelfde restricties als doelstellingsfunctie (1):

Om de verschillen te duiden maken we gebruik van gangbare beleggingscategorieën. Deze verdelen we onder in een drietal hoofdcategorieën, te weten hoogrentende leningen wereldwijd, aandelen wereldwijd en reële activa wereldwijd. In de laatste kolom is de maximum Sharpe ratio portefeuille (ook wel aangeduid als de meest gediversifieerde portefeuille) getoond die geconstrueerd is conform vergelijking 2. Verwachte rendementen, volatiliteiten en correlaties zijn geschat op basis van historische rendementen over een periode van 20 jaar.

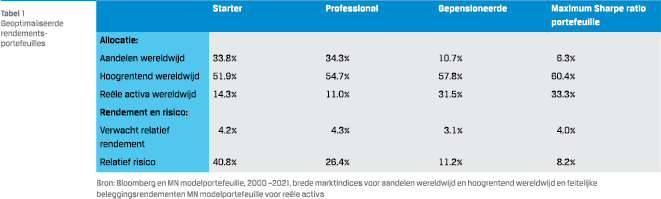De verhouding tussen het verwachte overrendement en risico is geoptimaliseerd voor de vier rendementsportefeuilles ten opzichte van hun benchmark. Voor een starter is de benchmark de verwachte pensioenuitkeringen met een renteduratie van vijftig jaar en meer. Daarentegen is de renteduratie van de verwachte uitkeringen van een gepensioneerde rondom vijftien jaar. De benchmark van de maximum Sharpe ratio portefeuille is de eendaags rente en het renterisico is derhalve verwaarloosbaar. Deze portefeuille is geconstrueerd conform doelstellingsfunctie (2). Het verschil in rentegevoeligheid is duidelijk te zien in de hoogte van het relatieve risico. De optimale rendementsportefeuille voor een starter heeft een risico ten opzichte van de verwachte uitkeringen van 40.8%. Dit komt door het renterisico voortvloeiend uit de hoge rentegevoeligheid van de verwachte uitkeringen.

Bij een starter en in iets mindere mate bij de professional is de renteduratie van de verwachte pensioenuitkeringen relatief lang. Opvallend is dat een geoptimaliseerde portefeuille in deze gevallen toch meer belegt in aandelen. Dit komt mede door de gehanteerde rendementsaannames. In onze analyse is het verwachte rendement op aandelen het hoogst. Daarentegen is de geoptimaliseerde portefeuille van een gepensioneerde vergelijkbaar met de maximum Sharpe ratio portefeuille. In beide gevallen is de rentegevoeligheid van de benchmark laag. Noemenswaardig is dat de allocatie naar reële activa in de maximum Sharpe ratio portefeuille begrensd is door de gehanteerde restrictie op illiquiditeit. De bovenstaande resultaten suggereren dat de invulling van de rendementsportefeuille leeftijdsafhankelijk is. Maar is dit wel het geval? Om dit verder te onderzoeken kijken we naar het totale rendements- en risicoprofiel van de beleggingsportefeuille van de drie deelnemers.

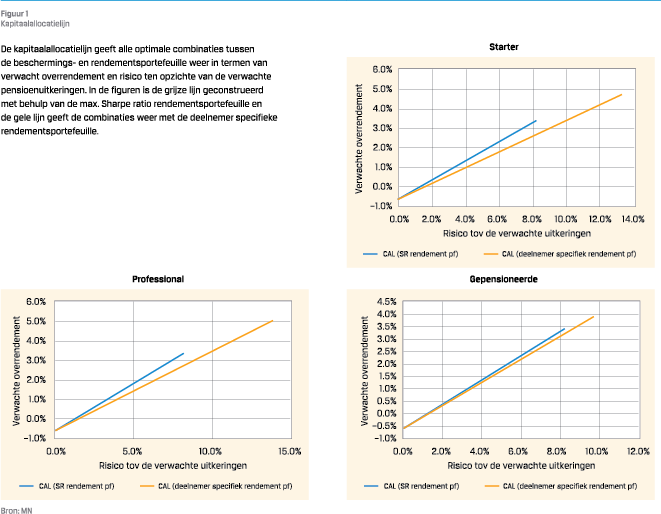Het totale risico van de beleggingsportefeuille van een deelnemer wordt bepaald door een allocatie naar de geoptimaliseerde rendementsportefeuille en de mate van renteafdekking. Voor kwantificering van het risico gaan we uit van een normale verdeling. De Capital Allocation Line (kapitaalallocatielijn, hierna afgekort als CAL) geeft de optimale uitruil weer tussen overrendement en risico voor alle mogelijke combinaties. Voor iedere deelnemer zijn er twee kapitaalallocatielijnen geconstrueerd. De een is op basis van de optimale Sharpe ratio portefeuille en de ander door middel van de rendementsportefeuille die geoptimaliseerd is voor de rentegevoeligheid van de verwachte uitkeringen van de deelnemer. Het verwachte overrendement en risico zijn geannualiseerd en uitgedrukt ten opzichte van de verwachte uitkeringen. Figuur 1 toont de resultaten. De beschermingsportefeuille is belegd in een combinatie van eendaags deposito en rentederivaten die op maat is geconstrueerd op basis van de rentegevoeligheid van de verwachte uitkeringen. Indien volledig belegd wordt in de beschermingsportefeuille dan is het risico ten opzichte van de verwachte uitkeringen nagenoeg nihil. De keerzijde is wel dat het verwachte overrendement negatief is. Dit komt door het verschil tussen eendaags deposito en de lange rente waarmee de verwachte pensioenuitkeringen contant gemaakt worden. De CAL is nagenoeg een rechte lijn omdat de historische lange termijn correlatie tussen zakelijke waarden en de rente vrij laag en rondom nul ligt.

OPTIMALE RENDEMENTSPORTEFEUILLE IS ONAFHANKELIJK VAN DE LEEFTIJD VAN DE DEELNEMER

Voor alle deelnemers zijn de rendement- en risicokenmerken van de portefeuille met een gestandaardiseerde rendementsportefeuille op basis van maximum Sharp ratio beter dan de beleggingsportefeuille waarvan de rendementsportefeuille is geoptimaliseerd op basis van de rentegevoeligheid van de verwachte pensioenuitkeringen. Dit verschil is groter naarmate de pensioenleeftijd verder in de tijd ligt. Hieruit kunnen we voorzichtig de conclusie trekken dat in de context van een totale portefeuille de optimale rendementsportefeuille leeftijdsonafhankelijk is en derhalve gestandaardiseerd kan worden. Is deze conclusie breder van toepassing of afhankelijk van de gehanteerde rendements- en risicocijfers?

 

TWEE FONDSEN SEPARATIE THEOREMA IN EEN MODERN JASJE

De moderne portefeuilletheorie (Markowitz, 1952) impliceert een beleggingsportefeuille voor alle beleggers die op basis van een kwadratische nutsfunctie bestaat uit een mix van een marktportefeuille met risicodragende instrumenten en een portefeuille die risicovrij is. Onder andere Tobin (1958), Cass en Stiglitz (1970), Merton (1973) en Ross (1978) deden uitgebreid onderzoek naar het concept van het twee fondsen separatie theorema. Hoewel het oorspronkelijke twee fondsen separatie theorema betrekking heeft op een risicovrije beleggingscategorie die vaak synoniem staat voor eendaags deposito, kan dit theorema ook toegepast worden in een asset liability management context (zie ook Martellini et al. 2012). Voor een stabiele pensioenuitkering moet een beleggingsportefeuille minimaal het rendement van de verwachte uitkeringen behalen. Dit vertaalt zich in de volgende doelstelling voor overrendement:

Hierin staat ro voor het verwachte overrendement van de beleggingsportefeuille. 𝔼(rP – rL) staat voor de verwachting van het portefeuille rendement (rP) minus het rendement van de verwachte uitkeringen (r0). μA en μL staan respectievelijk voor de verwachte rendementen van de verschillende beleggingscategorieën binnen de rendementsportefeuille en van de verwachte uitkeringen. Als laatste staat w voor de gewichten naar de verschillende beleggingscategorieën.

De optimalisatiefunctie van vergelijking 3 voor een belegger met een kwadratische nutsfunctie is gelijk aan:

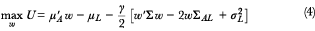
waarbij, γ de risico-aversie parameter van de deelnemer betreft. Dit houdt in dat er een uitruil wordt gedaan tussen het overrendement (μ' Aw – μL) en het risico ten opzichte van de verwachte uitkeringen w'Σw − 2wΣAL + σ2 L, waar γ dus bepaalt hoe groot de afkeer is ten opzichte van dat risico.

De oplossing van de optimalisatiedoelstelling (4) wordt gegeven door:

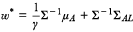
De oplossing geeft een optimale portefeuille die uit twee sub-portefeuilles bestaat. De een is overeenkomstig met de maximum Sharpe ratio rendementsportefeuille (hierna afgekort als RP) en de ander is een beschermingsportefeuille die maximaal gecorreleerd is met de verwachte uitkeringen (hierna afgekort als BP). We verkrijgen meer inzicht in de mix tussen deze twee sub-portefeuilles als we de Sharpe ratio en de correlatie tussen de portefeuille en de verwachte uitkeringen substitueren in de oplossing:

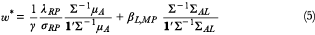
waarbij λRP de Sharpe ratio van de rendementsportefeuille RP betreft en βL,MP gelijk is aan de betacoëfficiënt tussen de beschermingsportefeuille BP en de verwachte uitkeringen.3 Uit oplossing (5) voor de optimalisatiefunctie in een ALM context (4) kunnen we de volgende conclusies trekken:

Allereerst is de constructie van de rendementsportefeuille onafhankelijk van de verwachte uitkeringen en risicohouding van een deelnemer en gelijk aan de maximum Sharpe ratio portefeuille van Markowitz. We gaan uit van een rendementsportefeuille in brede zin. Een eventuele rentevisie en de daaropvolgende rentepositionering vindt plaats in de rendementsportefeuille. De beschermingsportefeuille houden we hierdoor zuiver en richt zich volledig op de bescherming van de toekomstige pensioenuitkeringen. Het doel is dus om het risico van de beschermingsportefeuille ten opzichte van de verwachte uitkeringen te immuniseren. Op de tweede plaats is de allocatie naar de maximum Sharpe ratio portefeuille afhankelijk van de risicohouding van de deelnemer (γ) en de aantrekkelijkheid van de rendementsportefeuille welke gekwantificeerd is door de rendements/risico verhouding (λ RP/σRP ). Tot slot is de invulling van de beschermingsportefeuille afhankelijk van de rentegevoeligheid van de verwachte pensioenuitkeringen.

Deze bevindingen impliceren dat de samenstelling van de rendementsportefeuille leeftijdsonafhankelijk is en daarmee ook voor alle deelnemers gestandaardiseerd kan worden. Daarentegen is de invulling van de beschermingsportefeuille wel leeftijdsafhankelijk en vereist maatwerk. Het EDHEC Risk Institute onderschrijft deze conclusie in twee artikelen voor standaardisatie van de rendementsportefeuille en maatwerk van de beschermingsportefeuille (Badaoui et al. 2014 en Martellini et al., 2021).

 

KWALITATIEVE VERGELIJKING VAN GESTANDAARDISEERDE VERSUS LEEFTIJDSAFHANKELIJKE RENDEMENTSPORTEFEUILLE

Aan de hand van een uitwerking van de specifieke voordelen van een gestandaardiseerde en een leeftijdsafhankelijke rendementsportefeuille willen we de verschillen tussen beide portefeuilles meer inzichtelijk maken. Een gestandaardiseerde rendementsportefeuille voor alle leeftijdscohorten heeft schaalgrootte als belangrijkste voordeel. Een grote omvang van de rendementsportefeuille biedt meer diversificatiemogelijkheden. Vooral illiquide beleggingscategorieën zoals direct vastgoed, private equity of infrastructuur vereisen een bepaalde minimum omvang. Als er sprake is van verschillende rendementsportefeuilles kan de omvang daarvan ontoereikend zijn voor beleggingen in de illiquide categorieën. Eén rendementsportefeuille voor alle deelnemers verlaagt de uitvoeringskosten en kosten van het toezicht (governance) op de uitbesteding van het vermogensbeheer per euro onder beheer. Dit houdt in dat een gestandaardiseerde rendementsportefeuille efficiënter kan worden beheerd.

GESTANDAARDISEERDE RENDEMENTSPORTEFEUILLE VERLAAGT UITVOERINGSKOSTEN

Pensioenfondsen kunnen om valide redenen kiezen voor een leeftijdsafhankelijke rendementsportefeuille. Eén valide reden is ingegeven door een belangrijke aanname bij onze berekeningen, namelijk dat de verwachte Sharpe ratio onafhankelijk is van de beleggingshorizon en daardoor constant is. Deze aanname is overeenkomstig met de stelling van Merton (1969) dat de beleggingshorizon geen invloed heeft op de asset allocatie. Wanneer de hoogte van de Sharpe ratio afhankelijk is van de beleggingshorizon, waarbij de dynamiek van rendement en risico bijvoorbeeld voortgedreven wordt door mean reversion, dan voegt een leeftijdsafhankelijke invulling van de rendementsportefeuille waarde toe.

Campbell et al. (2005) onderzochten het effect van de beleggingshorizon op de samenstelling van de portefeuille. Middels de termijnstructuur van risicopremies verschaften de auteurs in het desbetreffende artikel inzicht in de uitruil tussen rendement en risico op verschillende beleggingshorizonnen. Naar onze mening is het duiden van een wereldbeeld voor een gepensioneerde met een gemiddelde beleggingshorizon tussen de tien jaar en vijftien jaar al moeilijk, laat staan verschillen aanbrengen tussen de leeftijdscohorten met een beleggingshorizon die kan oplopen tot meer dan vijftig jaar! Hoewel in ons theoretisch raamwerk de Sharpe ratio constant verondersteld werd, is deze aanname niet strikt noodzakelijk voor de twee fondsen theorema in een ALM context. Dequest et al. (2013) toonden aan dat de standaardisatie van de rendementsportefeuille nog steeds van toepassing is wanneer risicopremies stochastisch zijn en variëren met de economische conjunctuur. De optimale rendementsportefeuille blijft leeftijdsonafhankelijk, maar de samenstelling verandert wel naar gelang van de ontwikkelingen op de financiële markten.

Een starter kan meer risico dragen en is veelal ook bereid om dit hogere risico te nemen. Pensioen is nog ver weg en het opgebouwde pensioenkapitaal is aan het begin van zijn loopbaan nog relatief laag. Een volledige allocatie naar een maximum Sharpe ratio portefeuille kan in dit geval ontoereikend zijn om te kunnen voldoen aan de risicovoorkeur van een starter. Het leenrisico zou moeten worden opgeheven voor het bereiken van het gewenste rendement- en risicoprofiel van een starter. Het opheffen van de leenrestrictie is een mogelijkheid van het nieuwe pensioenstelsel bij de keuze voor een solidaire premieregeling. De effecten hiervan worden geïllustreerd in figuur 1. De optimale kapitaalallocatielijn stopt nabij een volatiliteit van 8 procent. Een hoger rendement- en risicoprofiel kan alleen bereikt worden door de lijn door te trekken door middel van een hefboom. Indien lenen niet wenselijk is, zou gekozen moeten worden voor een invulling van de rendementsportefeuille die een hoger rendement- en risicoprofiel, de facto een hogere allocatie naar aandelen, benadrukt maar gecorrigeerd voor risico minder optimaal samengesteld is.

 

INTEGRATIE VAN ESG: DRIE FONDSEN SEPARATIE THEOREMA

De laatste jaren is het belang van ‘verantwoord beleggen’ sterk toegenomen in de financiële wereld. De meeste pensioenfondsen in Nederland hebben inmiddels ook doelstellingen gedefinieerd op het gebied van duurzaamheid. Deze doelstellingen zijn op verschillende wijze in de portefeuille geïntegreerd en berusten meestal op het verminderen van het risicoprofiel van de portefeuille. De integratie van duurzaamheid in de portefeuille leidt doorgaans tot een afwijking van de maximum gediversifieerde returnportefeuille. Immers het behalen van een zo hoog mogelijk rendement gecorrigeerd voor risico is niet meer het hoofddoel. Het voeren van een duurzaam beleggingsbeleid is in dit geval voor de meeste deelnemers ook nutswaarde verhogend.

De integratie van duurzaamheid kan op verschillende manieren in het beleggingsbeleid tot uitdrukking komen. Pensioenfondsen kunnen bijvoorbeeld minder of helemaal geen geld investeren in bedrijven of overheden die niet voldoen aan de gestelde eisen op het gebied van ‘Environment, Social of Governance’ (ESG). Dit is een vorm van uitsluiting en aanpassing van het beleggingsuniversum. Daarentegen kunnen pensioenfondsen ook bepaalde beleggingen selecteren die een positieve impact hebben op de na te streven duurzaamheidsdoelen. Dit kan door meer of alleen maar te investeren in bedrijven of overheden die een positieve impact bewerkstelligen op bijvoorbeeld een of meerdere van de zeventien duurzame ontwikkelingsdoelstellingen van de Verenigde Naties. Wij abstraheren hier overigens van het beleidsinstrument beïnvloeding als gevolg van het eigenaarschap van de belegging (engagement). Dit beleidsinstrument raakt niet direct de samenstelling van de portefeuille.

In de beleggingsportefeuille kan de integratie van duurzaamheid worden vormgegeven op basis van de zogeheten ‘ESG-scores’. Dit zijn scores die aangeven in hoeverre een bedrijf of overheid ESG hebben geïmplementeerd in de bedrijfsvoering respectievelijk staatshuishouding. Beschikbaarheid van ESG-data neemt toe en steeds meer ratingsbureaus geven duurzaamheidsscores voor bedrijven en landen af. In dit artikel gaan we niet verder in op de wijze hoe de scores worden vastgesteld. We gaan ervan uit dat alle beleggingen voorzien kunnen worden van een ESG-score die objectief vastgesteld is en de duurzaamheid van een belegging weergeeft.

In onze portefeuille optimalisatie hebben we alleen rekening gehouden met risico en rendement. ESG-integratie vindt vaak plaats door ‘simpele’ methodes als het uitsluiten of het ‘downscalen’ van bepaalde beleggingen. Hieronder laten we zien op welke wijze ESG kan worden meegewogen in de portefeuille optimalisatie. De onderzoeksvraag daarbij is of ESG-integratie dan leidt tot maatwerk van de rendementsportefeuille?

ESG is in de portefeuille geïntegreerd door aanpassing van de volgende doelstellingsfunctie:

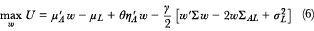
In vergelijking met de optimalisatiefunctie (4) die enkel gericht is op rendement en risico bevat de bovenstaande doelstelling een additionele term die de bijdrage van ESG-integratie aan de nutswaarde weergeeft. De rijvector ηA bevat scores die de ESG-voetafdruk in de beleggingen reflecteert. Hoe hoger de score des te duurzamer belegd wordt. We veronderstellen dat de benodigde horizon om de maatschappelijke impact te laten materialiseren en hoe groot deze impact is, versleuteld is in de ESG-score. De paramater θ geeft de preferentie weer voor ESG-integratie in de portefeuille. De oplossing van deze optimalisatiefunctie bestaat uit een drietal sub-portefeuilles:

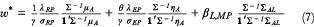
De eerste en laatste term van de oplossing is identiek aan oplossing (5): het betreft respectievelijk de maximum Sharpe Ratio rendementsportefeuille RP en de maximaal met de verwachte uitkeringen gecorreleerde beschermingsportefeuille BP. De tweede term is nieuw en geeft de maximum ESG geïntegreerde portefeuille (EP) weer. De allocatie naar de maximum ESG geïntegreerde portefeuille is afhankelijk van enerzijds de ESG-preferentie parameter θ en anderzijds de verhouding tussen de mate van ESG-integratie (totale ESG-score) en het risico van de maximum ESG-portefeuille EP (λEP). De uitruil tussen rendement en ESG-integratie wordt inzichtelijk gemaakt door de Sharpe ratio van de max. ESG geïntegreerde portefeuille EP (ΛEP) te relateren aan die van de rendementsportefeuille RP (λRP):

De term ρRP,EP is de correlatie tussen de maximum ESG geïntegreerde portefeuille EP en de maximum Sharpe ratio portefeuille RP. Omdat de correlatie maximaal 1 kan bedragen, is het rendement en risicoprofiel van de maximum ESG geïntegreerde portefeuille altijd gelijk of lager dan de maximum gediversifieerde portefeuille RP.

De drie fondsen separatie theorema impliceert dat naast een allocatie naar de beschermingsportefeuille die leeftijdsafhankelijk ingevuld moet worden, ook belegd wordt in twee portefeuilles, te weten de maximum ESG geïntegreerde portefeuille EP en de maximum gediversifieerde portefeuille RP. Beide portefeuilles zijn niet leeftijdsafhankelijk en kunnen dus gestandaardiseerd worden. ESG-integratie hoeft dus niet te leiden tot maatwerk van de rendementsportefeuille. Hoe sterk de ‘ESG-component’ wordt aangezet is onder andere afhankelijk van de ESG-preferentie van de deelnemers. Deze voorkeur kan worden aangezet of verminderd door de twee gestandaardiseerde rendementsportefeuilles in de juiste verhouding mee te nemen in het samenstellen van de portefeuille.

 

SUGGESTIES VERVOLGONDERZOEK

Een volgend onderzoek kan worden uitgevoerd naar de samenstelling van een gestandaardiseerde rendementsportefeuille voor een pensioenfonds. In de praktijk wordt een maximum Sharpe ratio portefeuille samengesteld op basis van verwachte rendements- en risicostatistieken (zie bijvoorbeeld de VBA risicostandaarden beleggingen 2021). Daarbij wordt rekening gehouden met de beleggingsbeginselen van pensioenfondsen, bepaalde risico’s die restrictief kunnen werken zoals een begrenzing van het liquiditeitsrisico en relevante wet- en regelgeving. Er zijn meerdere manieren om de benodigde invoervariabelen vast te stellen en te verwerken in de portefeuilleconstructie.

Een mogelijk startpunt voor de portefeuilleconstructie is een wereldwijde marktportefeuille. Hoewel de vaststelling van de wereldwijde marktportefeuille onderhevig is aan beschikbaarheid van data en aannames, brachten verschillende onderzoeken zo’n wereldwijde marktportefeuille in kaart. Zo verbeterde Doeswijk et al. (2019) hun eerdere onderzoek (zie Doeswijk et al. (2014)) met een breder beleggingsuniversum, door in hun studie ook private equity, hoogrentende obligaties, leveraged loans, inflatie-obligaties en obligaties van opkomende landen mee te nemen. De gewichten naar vastgoed en private equity werden hier wel onderschat omdat alleen werd uitgegaan van investeerbare indices. Gadzinski et al. (2021) losten dit op door in het universum ook niet beursgenoteerde beleggingen mee te nemen. Hierdoor neemt het gewicht van vastgoed en private beleggingen toe. Resulterend kwamen Gadzinski et al. (2021) uit op een redelijk gelijk gewogen samenstelling van een marktportefeuille. In tabel 2 is deze portefeuille opgenomen.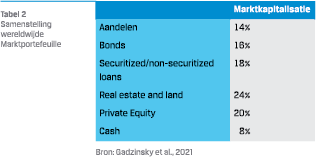

In dit artikel gaven we een onderbouwing voor het standaardiseren van de rendementsportefeuille. Deze rendementsportefeuille is leeftijdsonafhankelijk en maximaal gediversifieerd (maximum Sharpe ratio). Echter, de bepaling van de samenstelling van deze rendementsportefeuille is non-triviaal en een onderzoeksvraag die ons nog steeds in de greep houdt. Een wereldwijde marktportefeuille wordt doorgaans beschouwd als efficiënt waarin alle verwachtingen zijn gereflecteerd. Deze impliciete verwachtingen kunnen als referentiepunt gebruikt worden in de constructie van de maximum Sharpe ratio rendementsportefeuille (Doeswijk, Lam en Swinkels, 2014).

 

CONCLUSIES

Het meebewegen van de beleggingen met de levenscyclus van een deelnemer staat centraal in het nieuwe pensioenstelsel. De life-cycle theorie is bepalend voor de inrichting van de beleggingsportefeuille. Naarmate de pensioengerechtigde leeftijd van een deelnemer dichterbij komt, wordt het risicoprofiel van de beleggingsportefeuille geleidelijk afgebouwd. Het rendement- en risicoprofiel van de rendementsportefeuille kan ook op basis van deze theorie op dezelfde wijze worden verlaagd, maar dat is niet optimaal. Uit ons theoretische en kwantitatieve onderzoek blijkt juist dat een rendementsportefeuille gestandaardiseerd kan worden voor elke deelnemer. Dit is onze belangrijkste conclusie.

MATE VAN ESG-INTEGRATIE AFHANKELIJK VAN ESG-PREFERENTIE DEELNEMERS

De gestandaardiseerde rendementsportefeuille komt overeen met de maximum Sharpe ratio portefeuille en geeft het hoogste beleggingsrendement gecorrigeerd voor risico. Een gestandaardiseerde rendementsportefeuille is zeer passend voor pensioenfondsen met een solidaire pensioenregeling vanwege de mogelijkheid om de leenrestrictie op te heffen en het toepassen van een theoretisch beschermingsrendement voor de beschermingsportefeuille. Met dit laatste aspect zijn de beschermingsrendementen maximaal gecorreleerd met de verwachte pensioenuitkeringen. Overigens betekent een gestandaardiseerde rendementsportefeuille niet dat de samenstelling altijd vast staat. De samenstelling kan variëren op basis van relatieve voorkeur voor bepaalde beleggingen als gevolg van ontwikkelingen op de financiële markten.

ESG is een onlosmakelijk onderdeel van het beleggingsbeleid van de meeste institutionele beleggers. In ons theoretisch raamwerk hebben we het twee fondsen separatie theorema uitgebreid met een ESG geïntegreerde rendementsportefeuille. Het resultaat is een geoptimaliseerde beleggingsportefeuille op basis van rendement, risico en ESG. In theorie beschikt een deelnemer nu over drie ‘portefeuilles’, elk met een eigen doelstelling: beschermingsportefeuille ten behoeve van beheersing van het renterisico, gestandaardiseerde rendementsportefeuille die als doel heeft rendement te behalen en een gestandaardiseerde ESG geïntegreerde rendementsportefeuille die invulling geeft aan duurzaamheid. In de praktijk voeren pensioenfondsen nu een integraal ESG beleid voor de totale beleggingsportefeuille. Met de drie fondsen theorema kunnen pensioenfondsen nu een afweging maken tussen het leveren van ‘maatwerk’ op gebied van duurzaamheid voor de deelnemer of het continueren van de huidige integrale ESG aanpak voor alle deelnemers.

 

Literatuur

• Arnott, R., Sherrerd K., Wu L., 2013, The Glidepatch Illusion and Potential Solutions, The Journal of Retirement, Vol. 1 Issue 2 Fall 2013: 13-28
• Badaoui, S., Duguest, R., Martellini, L., Milhay, V., 2014, Dynamic Liability-Driven Investing Strategies: The Emergence of a New Investment Paradigm for Pension Funds?, An EDHECRisk Institute Publication February 2014.
• Cass, D., Stiglitz, J., 1970, The structure of investor preferences and asset returns, and separability in portfolio allocation: A contribution to the pure theory of mutual funds, Journal of Economic Theory, 2: 122-160.
• Campbell, J., Viceira, L., 2005, The term structure of the Risk-Return Trade-Off, Financial Analysts Journal, Vol. 61 1: 34-44.
• Dempster, M., Kloppers, D., Medova, E., Osmolovsky, I., Ustinov, P., 2016, Life-cycle Goal Achievement or Portfolio Volatility Reduction?, The Journal of Portfolio Management, Vol. 42 Issue 2 Winter 2016: 99-117.
• Dhillan, J., Ilmanen, A., Liew, J., 2016, Balancing on the Life Cycle: Target-Date Funds Need Better Diversification, The Journal of Portfolio Management, Vol. 41 Issue 4 Summer 2016: 12-27.
• Doeswijk, R. Q., T. W. Lam, and L. Swinkels. 2014. The global multi-asset market portfolio, 1959-2012, Financial Analysts Journal, Vol 70 Issue 2: 26-41.
• Doeswijk, R., Lam, Q., Swinkels, L., 2019, Historical Returns of the Market Portfolio, The Review of Asset Pricing Studies, Vol. 10 Issue 3: 521-567.
• Gadzinski, G., Schuller, M., Vacchino, A., 2021, The Global Market Portfolio, The Journal of Portfolio Management, Vol. 47 Issue 8: 151-163.
• Markowitz, H., 1952, Portfolio selection., Journal of Finance, Vol.7 No. 1: 77-91.
• Martellini, L., Milhau, V., 2012, Dynamic Allocation Decisions in the Presence of Funding Ratio Constraints, Journal of Pension Economics and Finance, Vol. 11 Issue 4: 549-580.
• Martellini, L., Milhau, V., Mulvey, J., Securing Replacement Income with Goal-Based Retirement Investing Strategies, An Edhec-Risk Institute Working Paper September 2021.
• Merton, R., 1969, Lifetime Portfolio Selection under Uncertainty: The Continuous Time Case, Review of Economics and Statistics, Vol. 51 No. 3: 247-257.
• Merton, R., 1973, An Intertemporal Capital Asset Pricing Model, Econometrica, Vol. 41 No. 5: 867-887.
• Pistorius, T.,2021, Life-cycle beleggen in het nieuwe pensioencontract: de theorie over de inzet van human capital en de nuances, VBA Journaal Nummer 148-Winter: 65-70.
• Ross, S., 1978, Mutual fund separation in financial theory – the separating distributions, Journal of Economic Theory, Vol. 17 Issue 2: 254-286.

Noten

1. Een apostrof achter een variabele geeft aan dat de matrix/ vector wordt getransponeerd, hier worden de elementen langs de hoofddiagonaal gespiegeld. Voor een vector houdt dit in dat een rijvector een kolomvector wordt en vice versa.
2. Zie DNB website: belegd vermogen voor risico pensioenfondsen 2021K4
3. De term λ RP/ σRP is gelijk aan µRP/σ2 RP = 1' Σ − 1µA

           en βL,MP=cov (L,MP)/σ2 L= 1' Σ − 1Σ AL

 

19 January 2023 in VBA Journaal door Kin Lee, Jan Oudenaarden en Michel Wetser