De nieuwe regelgeving voor pensioenfondsen bevat een sterke prikkel om de duration in de beleggingsportefeuille substantieel op te voeren, om zodoende de mismatch met verplichtingen te verkleinen. De solvabiliteitsontwikkeling met betrekking tot de nominale verplichtingen gemeten over een relatief korte periode van één jaar staat centraal bij deze nieuwe regels. Als we die twee uitgangspunten loslaten volgt echter een genuanceerder beeld. Los van de regelgeving lijkt hooguit een gedeeltelijke durationverlenging aantrekkelijk te zijn voor pensioenfondsen.
 Inleiding
Inleiding
Met het nieuwe financiële toetsingskader (nFTK) verdwijnt de vaste actuariële rekenrente van 4% voor de waardering van pensioenverplichtingen. De voorziening dient voortaan te worden berekend als de marktwaarde van de onvoorwaardelijke toezeggingen. In dit artikel gaan we uit van de in de praktijk meest voorkomende situatie, waarbij indexatie een voorwaardelijk karakter kent. Onder de onvoorwaardelijke toezeggingen vallen dan dus alleen de nominale rechten. Gegeven de lange looptijd van de pensioenuitkeringen zal de omvang van de voorziening zich dan op analoge wijze gaan ontwikkelen als de actuele waarde van een langlopende (nominale) obligatie. De duration van die overeenkomstige obligatie, een maatstaf voor de gevoeligheid voor renteveranderingen die sterk samenhangt met de looptijd, varieert doorgaans tussen 15 en 20 jaar.
Gangbare obligatieportefeuilles van pensioenfondsen kennen een duration van slechts zo’n 5 jaar. Bovendien vormen obligaties slechts een deel van de asset mix. Dit impliceert dat sprake is van een aanzienlijke mismatch tussen de actief- en passiefzijde van de balans van pensioenfondsen. Een durationmismatch van bijvoorbeeld 10 jaar houdt in dat de dekkingsgraad met circa 10% zal verslechteren (resp. verbeteren) bij een daling (resp. stijging) van de marktrente met 1%. Het substantieel verhogen van de duration in de beleggingsportefeuille ligt daarom voor de hand.
Oldenkamp en Roest (2004) pleiten er bijvoorbeeld voor om een aanzienlijk deel van de portefeuille in te vullen met cash-flow matching van de nominale verplichtingen. De kans op onderdekking na één jaar wordt op die wijze aanzienlijk verlaagd. Ook Heemskerk en Vos (2004) laten aan de hand van een voorbeeld zien dat de volatiliteit van de dekkingsgraad sterk kan worden gereduceerd, door de duration van de beleggingen op te voeren richting het niveau van de verplichtingen. Swinkels (2004) vindt vergelijkbare resultaten en wijst tevens op het gebruik van derivaten om de beoogde durationmatch op portefeuilleniveau te kunnen verwezenlijken. Omdat langlopende obligaties slechts beperkt voorhanden zijn, pleiten verder ook Kocken (2003) en Van Lieshout (2003) voor het gebruik van derivaten om renterisico’s af te dekken. Coppens, van der Hoek en Kuiters (2004) analyseren de toegevoegde waarde van derivaten in een ALM-context en vinden dat de kans op onderdekking met 30% tot 70% kan worden gereduceerd door renteswaps aan de portefeuille toe te voegen. In het Financieele Dagblad van 1 oktober 2004 pleit Kocken zelfs voor het volledig afdekken van renterisico’s met swaps.
Het laten aansluiten van de duration van de beleggingen bij die van de verplichtingen is optimaal vanuit het oogpunt van de solvabiliteitstoets in het nFTK, die bepalend is voor de omvang van de buffers die een pensioenfonds dient aan te houden. Deze toets kijkt naar het neerwaartse risico met betrekking tot de dekkingsgraad, uitgaande van (1) alleen de nominale (onvoorwaardelijke) verplichtingen en (2) een veronderstelde horizon van één jaar. Zowel het streven naar indexatie door het pensioenfonds, als de eventuele lange termijn dekkingsgraadrisico’s, zijn dus niet van belang voor de solvabiliteitstoets. In het vervolg van dit artikel bekijken we de gevolgen van het loslaten van deze twee veronderstellingen. Eerst gaan we in op de gevolgen van reële (geïndexeerde) verplichtingen in plaats van nominale verplichtingen en daarna op de gevolgen van een langere horizon. Uit onze analyses blijkt dat het drastisch opvoeren van de duration van de beleggingen dan opeens niet meer zo vanzelfsprekend is. Los van de regelgeving lijkt implementeren van meer dan een gedeeltelijke verlenging van de duration niet gewenst als het gaat om de uiteindelijke realisatie van de doelstellingen van een pensioenfonds.
Nominale versus reële verplichtingen
De solvabiliteitstoets kijkt alleen naar de nominale (onvoorwaardelijke) verplichtingen, maar voor de deelnemers is de beoogde indexatie van die rechten ook van groot belang. In feite zijn dus twee verschillende dekkingsgraden relevant voor een pensioenfonds: de dekkingsgraad op basis van alleen nominale toezeggingen (0% indexatie) en de dekkingsgraad op basis van reële verplichtingen (100% indexatie). Het beleggingsbeleid dient dan ook afgestemd te worden op deze beide dekkingsgraden.
In welke mate verandert de optimale durationkeuze als we de aandacht verschuiven van de nominale dekkingsgraad naar de reële dekkingsgraad? Om die vraag te beantwoorden introduceren we een analytische uitwerking van het ALM-probleem. De verplichtingen modelleren we daarbij als een obligatie (nominaal of juist reëel) met looptijd T en duration D. Het gewicht in zakelijke waarden beschouwen we ter vereenvoudiging als een gegeven, zodat we ons in de analyse volledig kunnen concentreren op beheersing van het renterisico. Verder is slechts een drietal kernaannames nodig om het basismodel af te kunnen leiden. Verderop zullen we overigens beargumenteren dat de conclusies waarschijnlijk niet wezenlijk veranderen als deze veronderstellingen worden gegeneraliseerd.
Aanname 1: De rendementen op zakelijke waarden zijn ongecorreleerd met alle renteveranderingen.
Aanname 2: Vastrentende beleggingsmogelijkheden beperken zich tot nominale obligaties, deposito’s en (nominale) renteswaps. Beleggingen in reële (geïndexeerde) obligaties of inflatieswaps laten we dus bijvoorbeeld buiten beschouwing. De nominale obligaties in onze analyse matchen exact met de nominale verplichtingen, en hetzelfde geldt voor de (longzijde van de) swaps.
Aanname 3: Verwachte toekomstige rentes destilleren we uit de forwardcurve. Ondanks dat rentes in de praktijk lang niet altijd daadwerkelijk naar de forwardcurve bewegen, vormt deze aanname naar onze mening het meest objectieve uitgangspunt. Zeker als we bedenken dat marktwaardering centraal staat bij de nieuwe regelgeving en de forwardcurve in feite de door de markt ingeprijsde toekomstige rentes representeert. Een implicatie van dit uitgangspunt is dat het verwachte rendement op alle vastrentende beleggingen identiek is. In het bijzonder is dus ook het verwachte rendement op een renteswap nihil. Omdat tevens het gewicht in zakelijke waarden gegeven is verondersteld, betekent dit dat we ons bij het bepalen van het optimale beleggingsbeleid verder kunnen richten op minimalisatie van het renterisico. Uitgaande van de forwardcurve brengt de keuze tussen deposito’s, lange obligaties en swaps immers geen rendementconsequenties met zich mee.
 Tabel 1 bevat een overzicht van definities van verschillende symbolen die we zullen gebruiken. Formule (1) in tabel 2 drukt het surplusrendement daarmee wiskundig uit. Hierbij veronderstellen we dat al het vermogen dat niet in zakelijke waarden zit in eerste instantie in deposito’s wordt belegd. De modellering van de renteswap volgt uit het feit dat deze beleggingstechnisch equivalent is met een long positie in een nominale obligatie plus een short positie in een (doorlopend) deposito. Ervan uitgaande dat de deposito’s bij een 1-jaars horizon risicoloos zijn (de 1-jaars rente is namelijk a priori een gegeven) geeft formule (2) de variantie van het surplusrendement weer. Hieruit kan worden afgeleid dat formule (3) de swapweging weergeeft die het risico minimaliseert.
Tabel 1 bevat een overzicht van definities van verschillende symbolen die we zullen gebruiken. Formule (1) in tabel 2 drukt het surplusrendement daarmee wiskundig uit. Hierbij veronderstellen we dat al het vermogen dat niet in zakelijke waarden zit in eerste instantie in deposito’s wordt belegd. De modellering van de renteswap volgt uit het feit dat deze beleggingstechnisch equivalent is met een long positie in een nominale obligatie plus een short positie in een (doorlopend) deposito. Ervan uitgaande dat de deposito’s bij een 1-jaars horizon risicoloos zijn (de 1-jaars rente is namelijk a priori een gegeven) geeft formule (2) de variantie van het surplusrendement weer. Hieruit kan worden afgeleid dat formule (3) de swapweging weergeeft die het risico minimaliseert.
Uitgaande van nominale verplichtingen volgt dat de optimale swapweging gelijk is aan Vnom / VA, ofwel de inverse van de nominale dekkingsgraad. De interpretatie van deze uitkomst is dat het risico wordt geminimaliseerd door het nominale renterisico van de verplichtingen volledig af te dekken. Deze uitkomst vormt een formulematige onderbouwing van onze eerdere constatering dat (volledige) eliminatie van de durationmismatch tussen beleggingen en verplichtingen optimaal is uit hoofde van de solvabiliteitstoets. Stel bijvoorbeeld dat de nominale dekkingsgraad 125% bedraagt. De waarde van de nominale verplichtingen is dan gelijk aan 80% van de waarde van de beleggingen, en dit percentage vormt ook de optimale weging van de swap. In een portefeuille met 40% zakelijke waarden zou deze uitkomst praktisch ingevuld kunnen worden door de resterende 60% van de portefeuille aan te wenden voor matching van de nominale verplichtingen, en het dan nog resterende renterisico te elimineren met behulp van 20% swaps.
 Bij reële verplichtingen verandert de optimale swapweging in (Vreal / VA) ρnom,real σreal / σnom. Ten opzichte van de situatie met nominale verplichtingen verandert de hoogte van de optimale swapweging dus door een drietal factoren:
Bij reële verplichtingen verandert de optimale swapweging in (Vreal / VA) ρnom,real σreal / σnom. Ten opzichte van de situatie met nominale verplichtingen verandert de hoogte van de optimale swapweging dus door een drietal factoren:
- Positief doordat (Vreal / VA) > (Vnom / VA): de waarde van reële verplichtingen is hoger dan die van nominale verplichtingen (uitgaande van nietnegatieve inflaties).
- Negatief doordat ρnom,real < 1: de correlatie tussen reële verplichtingen en nominale verplichtingen is per definitie niet perfect.
- Naar verwachting negatief doordat σreal / σnom < 1: reële obligaties zijn doorgaans minder volatiel dan nominale obligaties.
Afhankelijk van hoe sterk het eerste, positieve effect is ten opzichte van de twee overige negatieve effecten kan de optimale swapweging per saldo toenemen of juist dalen.
Met behulp van historische data kunnen we hierover een empirische uitspraak doen. Historische data omtrent reële obligaties is helaas slechts beperkt voorhanden, aangezien maar een klein aantal overheden dergelijke obligaties heeft geëmitteerd. Een relatief lange historie is beschikbaar voor het Verenigd Koninkrijk. Sinds eind jaren ’90 hebben ook de Verenigde Staten en Frankrijk een reële obligatiemarkt gecreëerd. In tabel 3 zijn de relevante statistieken voor deze markten vermeld. Met geschatte waarden van 0.47 tot 0.76 blijkt de correlatie tussen reële en nominale obligaties weliswaar kleiner dan één te zijn, maar nog steeds significant positief. De verhouding tussen de standaarddeviaties van reële en nominale obligaties is, met geschatte waarden van 0.59 tot 0.72, inderdaad kleiner dan één, zoals bij punt 3 werd gesteld.
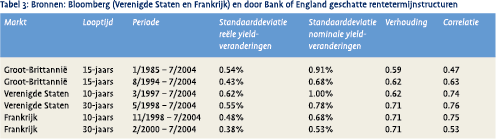 De beschikbare historische data heeft helaas betrekking op perioden waarin inflatie een dalende trend vertoonde of laag en stabiel was. We kunnen daarom niet nagaan of de geschatte parameters ook representatief zijn voor een periode van sterk oplopende inflatie. Bij gebrek aan betere informatie zullen we echter voor cijfermatige illustraties van de verschillende formules veronderstellen dat de cijfers in tabel 3 betrouwbare schattingen voor de toekomst vormen.
De beschikbare historische data heeft helaas betrekking op perioden waarin inflatie een dalende trend vertoonde of laag en stabiel was. We kunnen daarom niet nagaan of de geschatte parameters ook representatief zijn voor een periode van sterk oplopende inflatie. Bij gebrek aan betere informatie zullen we echter voor cijfermatige illustraties van de verschillende formules veronderstellen dat de cijfers in tabel 3 betrouwbare schattingen voor de toekomst vormen.
Ervan uitgaande dat de oorspronkelijk veronderstelde nominale dekkingsgraad van 125% equivalent is met een reële dekkingsgraad van 85%, en uitgaande van een σreal/ σnom verhouding van 0.6 en een correlatie ρnom,real van eveneens 0.6, volgt dat de optimale swapweging met betrekking tot de reële verplichtingen 42% bedraagt. Dit is bijna een halvering ten opzichte van het optimale niveau van 80% bij nominale verplichtingen. Deze afname valt te verklaren uit het feit dat nominale obligaties geen perfecte hedge bieden voor inflatierisico, dat een essentieel element vormt van de reële verplichtingen.
 In combinatie met de 40% zakelijke waarden en 60% deposito’s die we als vertrekpunt namen, komt de nieuwe portefeuille uit op 40% zakelijke waarden, 42% obligaties die matchen met de nominale verplichtingen en 18% kas. Dit houdt nog steeds een substantiële verhoging van de duration ten opzichte van een traditionele portefeuille in, maar lang niet zo sterk als we eerder vonden met de nominale verplichtingen als uitgangspunt. Deze durationverlenging kan in principe zelfs zonder swap overlay, dus met uitsluitend fysieke obligaties, worden bereikt.
In combinatie met de 40% zakelijke waarden en 60% deposito’s die we als vertrekpunt namen, komt de nieuwe portefeuille uit op 40% zakelijke waarden, 42% obligaties die matchen met de nominale verplichtingen en 18% kas. Dit houdt nog steeds een substantiële verhoging van de duration ten opzichte van een traditionele portefeuille in, maar lang niet zo sterk als we eerder vonden met de nominale verplichtingen als uitgangspunt. Deze durationverlenging kan in principe zelfs zonder swap overlay, dus met uitsluitend fysieke obligaties, worden bereikt.
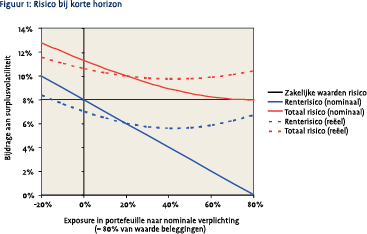
Figuur 1 toont het surplusrisico, opgesplitst naar zakelijke waarden risico en renterisico, bij verschillende maten van durationverlenging. Aanvullende parameterveronderstellingen hierbij zijn: σzw = 20%, σnom = 10%, σreal = 6%. De figuur illustreert nogmaals dat volledige matching optimaal is uitgaande van de nominale verplichtingen, maar dat slechts ongeveer halve matching optimaal is uitgaande van de reële verplichtingen. Met andere woorden, volledige matching van het nominale renterisico is optimaal vanuit het oogpunt van de solvabiliteitstoets, maar suboptimaal vanuit het oogpunt van de reële verplichtingen die het pensioenfonds in het algemeen daadwerkelijk nastreeft. Daarbij geldt wel dat de mate van suboptimaliteit, in termen van het extra risico, beperkt is. Omgekeerd geldt echter ook dat uitgaande van de nominale verplichtingen de mate van suboptimaliteit van slechts een halve matching eveneens beperkt is.
Korte versus lange horizon
De solvabiliteitstoets beperkt zich niet alleen tot de nominale (onvoorwaardelijke) verplichtingen, maar hanteert ook een horizon van slechts één jaar. De aandacht verschuift hierdoor naar het beheersen van de korte termijn (rente)risico’s, waarbij het gevaar dreigt dat de lange termijn risico’s uit het oog worden verloren. Voor vastrentende beleggingen geldt dat het risico afhankelijk is van de horizon. Zo kent een 20-jaars zerocoupon obligatie een substantieel renterisico op korte termijn, maar met een beleggingshorizon van 20 jaar vormt deze obligatie juist de risicovrije belegging. De nominale verplichtingen kennen op lange termijn dus ook geen renterisico. Andersom geldt dat een deposito risicoloos is op korte termijn, terwijl de cumulatieve opbrengst van 20 jaar lang deposito’s doorrollen juist onzeker is. Aangezien swaps het economische risico van een shortpositie in een doorlopend deposito met zich meebrengen, zou een swap overlay op lange termijn dus juist risicoverhogend kunnen werken!
Hoe kunnen we het risico van verschillende vastrentende beleggingsvormen op lange termijn kwantificeren? Schattingen maken op basis van lange historische perioden is problematisch vanwege het beperkte aantal beschikbare onafhankelijke observaties. Een alternatief is om op basis van kortere termijn data een model te schatten en daarmee mogelijke lange termijn ontwikkelingen te simuleren. Het maken van diverse veronderstellingen is daarbij onvermijdelijk. Lange termijn risico’s kunnen echter ook rechtstreeks worden afgeleid uit onze eerdere algemene aannames, dus zonder modellen te schatten of gebruik te maken van lange historische perioden.
Aanname 3 luidde dat rentecurves naar verwachting naar de bijbehorende forwardcurves bewegen. Dit impliceert voor iedere vastrentende belegging dat het verwachte rendement bij een horizon van N jaar gelijk is aan de initiële N-jaars rente (yield). Concreet is het verwachte rendement over het eerste jaar dus gelijk aan de initiële 1-jaars rente, r[0,1],t=0. Verder geldt dat het verwachte (ingeprijsde) rendement vanaf einde eerste jaar tot einde looptijd aanvankelijk gelijk is aan de initiële forwardrente, f[1,T],t=0. De nieuwe verwachting na afloop van het eerste jaar is echter de actuele yield, y[1,T],t=1, waardoor de rendementperspectieven van het fonds zijn verbeterd of juist verslechterd. Aan deze mutatie in het door de markt ingeprijsde verwachte rendement kan, uitgaande van een duration die dan circa 1 jaar korter is geworden, een waarde van bij benadering (D–1) (y[1,T],t=1 – f[1,T],t=0) worden toegekend.
Essentieel is nu dat we voor elk vastrentend instrument deze waardemutatie optellen bij het feitelijke rendement over het eerste jaar, om zo niet alleen de korte termijn, maar tevens de lange termijn consequenties van marktontwikkelingen mee te nemen. In feite nemen we op deze wijze een soort extra asset mee op de balans, namelijk de door de markt ingeprijsde toekomstige opbrengsten tot einde looptijd op de verschillende vastrentende instrumenten. De verandering van de marktwaarde van dit asset geeft weer hoe de lange termijn rendementperspectieven van het fonds veranderen. In tabel 4 is dit uitgewerkt voor de verschillende beleggingsinstrumenten. Hieruit blijkt bijvoorbeeld dat, als we het lange termijn effect meenemen, nominale obligaties conform de intuïtie risicovrij zijn, maar deposito’s niet. De omvang van het risico van deposito’s blijkt gelijk te zijn aan het korte termijn risico van een shortpositie in nominale obligaties. Met andere woorden, de mate waarin bijvoorbeeld de lange termijn rendementperspectieven van deposito’s verbeteren door een stijging van de lange rente, is gelijk aan de korte termijn winst die deze gebeurtenis met zich meebrengt voor een shortpositie in nominale obligaties.
We richten onze aandacht nu op de minimalisatie van het dekkingsgraadrisico inclusief de lange termijn effecten. Hierbij kijken we ook weer apart naar de situatie met nominale verplichtingen en de situatie met reële verplichtingen. Ter vereenvoudiging van de formules drukken we voor deze analyse het surplusrendement iets anders uit, namelijk door als vertrekpunt te nemen om al het vermogen dat niet in zakelijke waarden zit te beleggen in matching nominale obligaties in plaats van in deposito’s. Zie formule (4) in tabel 2.
 Uitgaande van nominale verplichtingen, en gegeven de constateringen in tabel 4, is het lange termijn risico van het surplusrendement equivalent met het korte termijn risico van de positie die is weergeven in formule (5). Formule (6) geeft de variantie van deze positie weer, waaruit direct volgt dat het minimale risico wordt bereikt bij geen swaps toevoegen aan de portefeuille, zoals weergegeven in formule (7). Met andere woorden, uitgaande van nominale verplichtingen is het optimale lange termijn beleggingsbeleid om alleen het vermogen dat niet in zakelijke waarden zit te matchen met de verplichtingen en dus niet aanvullend het resterende nominale renterisico af te dekken met swaps. Dit kan worden verklaard uit het feit dat langlopende obligaties op lange termijn risicovrij zijn, maar instrumenten met korte rente exposure, zoals deposito’s en swaps, niet. Figuur 2 bevat een grafische illustratie, gebaseerd op dezelfde parameterveronderstellingen als voor figuur 1.
Uitgaande van nominale verplichtingen, en gegeven de constateringen in tabel 4, is het lange termijn risico van het surplusrendement equivalent met het korte termijn risico van de positie die is weergeven in formule (5). Formule (6) geeft de variantie van deze positie weer, waaruit direct volgt dat het minimale risico wordt bereikt bij geen swaps toevoegen aan de portefeuille, zoals weergegeven in formule (7). Met andere woorden, uitgaande van nominale verplichtingen is het optimale lange termijn beleggingsbeleid om alleen het vermogen dat niet in zakelijke waarden zit te matchen met de verplichtingen en dus niet aanvullend het resterende nominale renterisico af te dekken met swaps. Dit kan worden verklaard uit het feit dat langlopende obligaties op lange termijn risicovrij zijn, maar instrumenten met korte rente exposure, zoals deposito’s en swaps, niet. Figuur 2 bevat een grafische illustratie, gebaseerd op dezelfde parameterveronderstellingen als voor figuur 1.
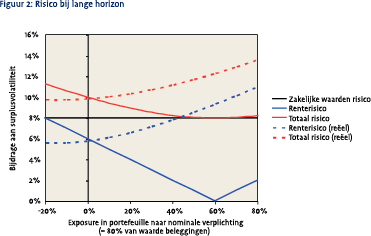 Uitgaande van reële verplichtingen is het lange termijn risico van het surplusrendement equivalent met het korte termijn risico van de positie in formule (8). Formule (9) geeft de variantie van deze positie weer. Formule (10) toont de resulterende optimale, ofwel risico minimaliserende oplossing, wswap = (Vreal / VA) (ρnom,real σreal / σnom – 1). Omdat empirisch lijkt te gelden dat ρnom,real σreal / σnom < 1 (zie eerder) komt dit neer op een negatief gewicht voor de swap. In combinatie met de uitgangsportefeuille houdt dit in dat het optimaal is om slechts een deel van het vermogen dat niet in zakelijke waarden zit te matchen met verplichtingen, en het restant in deposito’s te beleggen. De optimale mate van nominale matching kan zelfs per saldo negatief uitpakken als we uitgaan van de reële verplichtingen op lange termijn! Dit blijkt bijvoorbeeld uit de empirische illustratie in figuur 2, waarin de optimale portefeuille bestaat uit 40% zakelijke waarden, 60% deposito’s en daarnaast nog een 15% shortpositie in de swap die de nominale verplichtingen uitruilt tegen deposito’s.
Uitgaande van reële verplichtingen is het lange termijn risico van het surplusrendement equivalent met het korte termijn risico van de positie in formule (8). Formule (9) geeft de variantie van deze positie weer. Formule (10) toont de resulterende optimale, ofwel risico minimaliserende oplossing, wswap = (Vreal / VA) (ρnom,real σreal / σnom – 1). Omdat empirisch lijkt te gelden dat ρnom,real σreal / σnom < 1 (zie eerder) komt dit neer op een negatief gewicht voor de swap. In combinatie met de uitgangsportefeuille houdt dit in dat het optimaal is om slechts een deel van het vermogen dat niet in zakelijke waarden zit te matchen met verplichtingen, en het restant in deposito’s te beleggen. De optimale mate van nominale matching kan zelfs per saldo negatief uitpakken als we uitgaan van de reële verplichtingen op lange termijn! Dit blijkt bijvoorbeeld uit de empirische illustratie in figuur 2, waarin de optimale portefeuille bestaat uit 40% zakelijke waarden, 60% deposito’s en daarnaast nog een 15% shortpositie in de swap die de nominale verplichtingen uitruilt tegen deposito’s.
Waarom is het bij reële verplichtingen optimaal om de nominale renterisico’s niet te matchen, en zelfs deposito’s aan te houden? De verklaring is dat nominale matching geen enkele inflatiebescherming biedt, terwijl inflatie op lange termijn juist de grote onzekere factor achter de reële verplichtingen is. De door de markt verwachte (ingeprijsde) inflatie kan bijvoorbeeld toenemen doordat de nominale rente oploopt en de reële rente niet. Hogere nominale rentes gaan in ons analysekader echter samen met hogere verwachte toekomstige (ingeprijsde) rentes voor depositobeleggers. Dit verklaart onze bevinding dat deposito’s een betere match met de reële verplichtingen bieden.
Aannames opnieuw beschouwd
Hoe essentieel zijn de gemaakte veronderstellingen om tot bovenstaande resultaten te komen? Om deze vraag te beantwoorden gaan we nader in op elk van de aannames 1, 2 en 3.
Aanname 1: Zakelijke waarden zijn ongecorreleerd met alle renteveranderingen
Deze aanname kan betrekkelijk eenvoudig worden losgelaten, door de relevante correlaties ongelijk aan nul te veronderstellen. In een bijlage, die op aanvraag beschikbaar is bij de auteur, is uitgewerkt hoe de optimale swapwegingen in dat geval veranderen. De effecten zijn op zich logisch. Als zakelijke waarden bijvoorbeeld verondersteld worden een zekere mate van hedge voor de nominale verplichtingen te vormen, hoeven de nominale renterisico’s in het resterende deel van de portefeuille navenant minder afgedekt te worden.
In de praktijk bestaan de zakelijke waarden vaak grotendeels uit aandelen. Omdat aandelen een claim op een lange reeks toekomstige (deels inflatiebestendige?) cash-flows inhouden, wordt aan aandelen vaak theoretisch een hoge duration toegedicht. Bekend is echter dat die hoge duration empirisch nauwelijks zichtbaar is, en dat de correlatie tussen aandelen en obligaties in sommige perioden zelfs negatief is. Aandeelrendementen bewegen historisch ook niet of nauwelijks mee met de ontwikkeling van de korte rente, dus ook voor dat renterisico bieden zij geen bescherming. Expliciet rekening houden met de empirische samenhang tussen zakelijke waarden en renteveranderingen lijkt daarom al met al niet tot wezenlijk andere resultaten te leiden.
Aanname 2: Reële obligaties laten we buiten beschouwing als beleggingsmogelijkheid
Beleggingen in reële (geïndexeerde) obligaties of inflatieswaps zijn tot nu toe buiten beschouwing gelaten ter vereenvoudiging en omdat deze vanwege een beperkt aanbod op macro-economisch niveau (vooralsnog) slechts van marginaal belang zijn voor de pensioensector als geheel. Dat neemt niet weg dat het hier een zeer interessante beleggingsmogelijkheid betreft, waarmee de reële renterisico’s sterk kunnen worden gereduceerd. Dit kan pleiten voor een forse allocatie naar reële obligaties. Vanuit het oogpunt van de nominale verplichtingen, en dus de solvabiliteitstoets in het bijzonder, zijn aan de inflatie gerelateerde beleggingen echter weer minder interessant. Deze effecten kunnen vrij eenvoudig expliciet worden gemaakt door het model uit te breiden met beleggingen in reële obligaties, maar ook deze extensie valt buiten het bestek van dit artikel.
Aanname 3: De verwachte toekomstige rentecurve is gelijk aan de forwardcurve
Vanuit het oogpunt van marktwaardering is het op zich een logisch uitgangspunt om door de markt ingeprijsde rentes, ofwel forwardrentes, te gebruiken als verwachting voor toekomstige rentes. Met name de implicatie dat iedere vastrentende belegging een identiek verwacht rendement biedt, lijkt echter strijdig met de empirische observatie van een risicopremie op bijvoorbeeld obligaties ten opzichte van deposito’s. Rekening houden met zo’n risicopremie heeft voor de korte horizon analyses geen consequenties voor het risico. Voor de lange horizon analyses geldt hetzelfde als we veronderstellen dat de risicopremie constant (niet-stochastisch) is. Merk op dat langlopende obligaties nog altijd risicovrij zijn bij een lange horizon, en dat de hoogte van de risicopremie in dit geval betrekking heeft op de mate waarin het (onzekere) rendement van deposito’s naar verwachting lager zal uitvallen. Wel geldt dat de portefeuilles met minimaal risico niet langer automatisch optimaal zijn, omdat de rendementdimensie ook van belang wordt. Naarmate meer belang aan rendement wordt gehecht, kan dat bijvoorbeeld pleiten voor meer obligaties en/of swaps in plaats van deposito’s. Op basis van lange historische reeksen lijkt de risicopremie van obligaties ten opzichte van deposito’s overigens relatief klein te zijn. Zo vinden Dimson et al. (2002) voor de Nederlandse markt een gemiddelde risicopremie van obligaties van slechts 0.4% over de periode 1900-2000 en 0.3% over de periode 1950-2000.
Ten slotte kan nog getwist worden over de vraag of we representatieve parameters hebben gekozen voor de cijfermatige voorbeelden. De voorbeelden dienen echter primair slechts ter illustratie van de formules, die een algemeen karakter hebben.
Conclusies
De solvabiliteitstoets in het nFTK richt zich op de nominale (onvoorwaardelijke) verplichtingen en hanteert daarbij een relatief korte horizon van één jaar. Minimalisatie van het ALM-renterisico uit hoofde van deze toets houdt in dat het nominale renterisico van de verplichtingen volledig moet worden afgedekt. Als we de aandacht echter verleggen naar de reële verplichtingen of de lange termijn, wat meer aansluit bij de werkelijke doelstelling van een pensioenfonds, geniet een minder dan volledige matching van de nominale rentegevoeligheden de voorkeur. Kijkend naar de combinatie van reële verplichtingen en de lange termijn is het zelfs mogelijk dat een negatieve duration naar nominale rentes in de beleggingsportefeuille optimaal is! Dit kan worden verklaard uit het feit dat nominale obligaties (of swaps) geen goede hedge vormen voor de inflatierisico’s, die op lange termijn de grootste bedreiging voor de indexatieambitie vormen.
Hoe dient een pensioenfonds nu in de praktijk om te gaan met renterisico? Hiertoe zal het fonds eerst de keuze moeten maken of het zich primair wil concentreren op de nominale of reële verplichtingen, en op de korte of lange termijn. Als de solvabiliteitstoets knellend is, bijvoorbeeld in geval van een lage dekkingsgraad, kan het fonds zich waarschijnlijk weinig anders permitteren dan concentreren op het renterisico van de nominale verplichtingen op korte termijn. Volledig of grotendeels afdekken van de nominale renterisico’s ligt dan voor de hand. Fondsen met meer bewegingsvrijheid kunnen zich hier echter in meer of mindere mate aan onttrekken, en zich meer richten op de reële verplichtingen op lange termijn. Beheersen van inflatierisico is dan essentieel, en daarbij is matching van nominale renterisico’s minder aantrekkelijk, of zelfs ronduit onaantrekkelijk.
Referenties
- Coppens, M., M. Kuiters en J. van der Hoek (2004), Risicobeheersing onder fair value, VBA-Journaal, najaar 2004, nr. 3, p.18-25
- Dimson, E., P. Marsh en M. Staunton (2002), Triumph of the optimists, Princeton University Press
- Heemskerk, F. en M. Vos (2004), “Gevolgen marktwaardering verplichtingen op beleid pensioenfondsen”, VBA Journaal, zomer 2004, nr. 2, p.27-31
- Kocken, T. (2003), “Scherper aan de wind zeilen onder fair value”, The Financial Analyst, jaargang 4, nr. 7, 2003, p.51-55
- Van Lieshout, L. van (2003), “Dynamisch beleggingsbeleid voor pensioenfondsen”, The Financial Analyst, jaargang 4, nr. 7, 2003, p.44-47
- Oldenkamp, K.P.B. en M. Roest (2004), “Nieuwe ronde, nieuwe risico’s, nieuwe kansen”, Nederlands Pensioen- & Beleggingsnieuws, zomer 2004, nr. 1, p.23-25
- Swinkels, L. (2004), “A new benchmark for pension funds”, IPE Netherlands, August 2004, p.32-33
in VBA Journaal door David Blitz
