 Het afdekken van renterisico
Het afdekken van renterisico
In de afgelopen maanden hebben veel pensioenfondsen gemerkt dat hun renterisico minder goed was afgedekt dan zij dachten. De oorzaak hiervan verschilt per pensioenfonds. Vaak was de afdekking van curverisico en/of van convexiteit onvoldoende. Ook hadden veel pensioenfondsen het risico van hun pensioenverplichtingen (op swaprentes) afgedekt met obligaties, die tijdens de kredietcrisis nogal afwijkende prijsveranderingen ondergingen.
Er is nog een verklaring, die weinig bekend is weliswaar, maar die voor vrijwel alle pensioenfondsen geldt. Deze verklaring is gelegen in een verkeerde toepassing van duration matching vanwege een verkeerde specificatie van het renterisico.
In dit artikel hopen we een bijdrage te leveren aan de kwaliteitsverbetering van renteafdekkingen. We laten zien waarom de alom gebruikte modified duration (MD) van de verplichtingen2 niet de juiste maat is voor het renterisico van pensioenfondsen. Afdekkingen van renterisico die gebaseerd zijn op MD kunnen zelfs averechts werken omdat ze teveel of juist te weinig afdekken. Vervolgens leiden we af hoe de MD kan worden aangepast om een adjusted liability duration (ALD) te berekenen die voor pensioenfondsen wel leidt tot de gewenste afdekking. Ook voor de convexity leiden we een adjusted liability convexity (ALC) af. De beschreven effecten worden wiskundig onderbouwd in de appendices.
Het traditioneel afdekken van de duration gap
Het is onder pensioenfondsen gangbaar om voor de duration matching het renterisico te beoordelen als het verschil in de rentegevoeligheid van beleggingen en verplichtingen. Dit wordt de duration gap genoemd. Het verschil tussen de waarde van de beleggingen en de waarde van de verplichtingen is het surplus van het pensioenfonds. De duration gap is dus de rentegevoeligheid van het surplus en bij volledige afdekking van het surplus (‘dichtzetting van de duration gap’) worden dan rentedragende beleggingen en/of een derivaten-overlay gekozen die de gewenste afdekking geven.
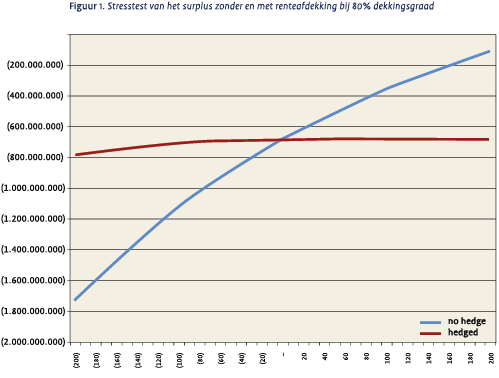 Laten we eens kijken hoe een dergelijke afdekking voldoet voor een voorbeeld-pensioenfonds. Stel dat dit pensioenfonds momenteel een dekkingsgraad van 80% heeft en een 30/70 aandelen/vastrentend mix heeft gekozen (een voorbeeld van een pensioenfonds met een hogere dekkingsgraad komt later aan de orde). Figuur 1 laat het renterisico van dit niet afgedekte pensioenfonds zien.
Laten we eens kijken hoe een dergelijke afdekking voldoet voor een voorbeeld-pensioenfonds. Stel dat dit pensioenfonds momenteel een dekkingsgraad van 80% heeft en een 30/70 aandelen/vastrentend mix heeft gekozen (een voorbeeld van een pensioenfonds met een hogere dekkingsgraad komt later aan de orde). Figuur 1 laat het renterisico van dit niet afgedekte pensioenfonds zien.
Het renterisico wordt getoond aan de hand van de waarde van het surplus (in dit geval negatief vanwege het dekkingstekort) bij verschillende (parallelle) renteveranderingen, van -200 bp tot + 200bp. Merk op dat het pensioenfonds zou profiteren van een rentestijging.
Stel dat we het renterisico van het pensioenfonds vervolgens zouden afdekken (tegen parallelle bewegingen van de rentecurve) met één renteswap en dat we hiervoor een 30-jaars receiver swap kiezen. Zie wederom figuur 1 voor het renterisico van het nu wel afgedekte pensioenfonds.
Merk op dat, behoudens de convexiteit, de waarde van het surplus inderdaad goed is afgedekt. Overigens, het risico op niet-parallelle veranderingen in de rentecurve is niet afgedekt, maar met een uitbreiding van de afdekking van één swap naar een combinatie van een aantal swaps met verschillende looptijden is dit betrekkelijk eenvoudig te realiseren.
 De hamvraag: is het pensioenfonds nu correct afgedekt?
De hamvraag: is het pensioenfonds nu correct afgedekt?
Is het renterisico van het pensioenfonds nu daadwerkelijk correct afgedekt? Doorgaans immers stopt men hier de analyse en het ontwerp van een afdekking, en wordt door de tijd (en bijvoorbeeld nieuwe pensioenopbouw, premie inflow, pensioenbetalingen en mogelijke overdrachten) de controle op de effectiviteit daarvan vaak vertroebeld. Is de graadmeter – zijnde de dekkingsgraad – van het fonds nu immuun tegen rentefluctuaties?
Het vlakke verloop van het surplus in figuur 1 suggereert dat het renterisico inderdaad goed is afgedekt. Echter, voor het pensioenfonds blijken de problemen nog niet te zijn opgelost. Om dit in te zien moeten we kijken naar de dekkingsgraad.
De (nominale) dekkingsgraad is voor een pensioenfonds vaak een belangrijker gegeven dan de (absolute) waarde van het surplus. Zo is de dekkingsgraad leidend in discussies over aanpassingen in beleggingsbeleid en toeslagverlening; twee factoren die de solvabiliteit (het surplus) van een pensioenfonds sterk beïnvloeden.
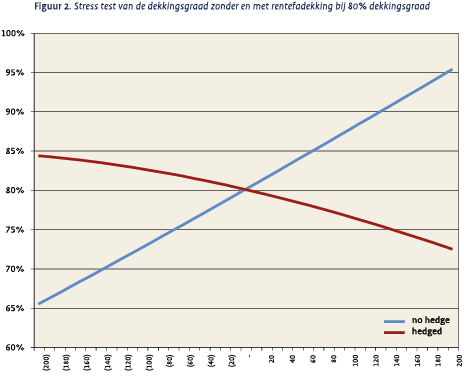
Laten we eens kijken hoe hoog de dekkingsgraad is bij de verschillende renteniveaus. Figuur 2 laat dit zien voor het nog niet afgedekte pensioenfonds en na de afdekking met de eerder gebruikte 30 jaars swap.
In figuur 2 zien we dat de dekkingsgraad van het nog niet afgedekte pensioenfonds stijgt bij stijging van de rente, en vice versa. Deze grafiek van de dekkingsgraad is vergelijkbaar met figuur 1 inzake het surplus.
Na het installeren van de renteswap zien we dat de afdekking die zo goed werkt voor het surplus (vgl. figuur 1) niet werkt voor de dekkingsgraad. Het is zelfs zo dat de afdekking averechts werkt: bij stijging van de rente zal nu de dekkingsgraad zelfs gaan dalen! Zonder meer een ongewenste situatie en ook een gevaarlijke indien het pensioenfonds zich hier niet van bewust zou zijn.
Uiteraard is het probleem dat we hier tonen niet alleen een probleem voor ons voorbeeld-pensioenfonds met z’n 80% dekkingsgraad. Ook voor hogere of lagere percentages van dekkingstekort speelt dit probleem en hoe hoger (of hoe lager) de dekkingsgraad des te zwaarder de impact. Ook is het niet zo dat het probleem er alleen is als een pensioenfonds 100% van z’n renterisico probeert af te dekken zoals in het voorbeeld. Vaak kiezen pensioenfondsen niet voor volledige afdekking, maar voor een percentage van de verplichtingen dat afgedekt dient te worden.
 In dit geval wordt in feite een deel van het surplus afgedekt.
In dit geval wordt in feite een deel van het surplus afgedekt.
In zijn algemeenheid kan worden gesteld dat als een pensioenfonds met een dekkingstekort z’n renterisico afdekt op de traditionele, hierboven beschreven wijze, er meer wordt afgedekt dan men eigenlijk wil. Het gevolg hiervan is dat als de rente gaat stijgen, de dekkingsgraad van het pensioenfonds zich opeens ongunstig zal ontwikkelen.
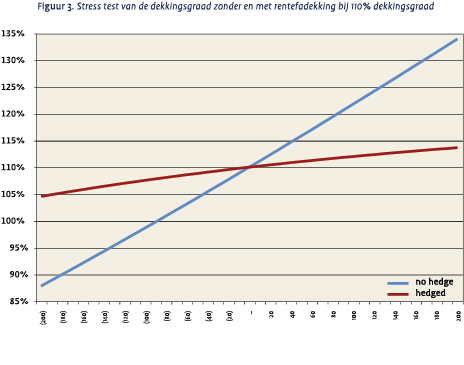
Het omgekeerde geldt voor pensioenfondsen met een dekkingsoverschot: zij zullen minder afgedekt zijn dan bedoeld en daardoor juist bij rentedaling de dekkingsgraad zich slechter zien ontwikkelen dan verwacht.
We illustreren dit nog even aan de hand van een voorbeeld pensioenfonds met 110% dekkingsgraad en een 40/60 aandelen/vastrentend mix. In figuur 3 laten we wederom de situatie zien voor het nog niet afgedekte pensioenfonds en na de afdekking met een 30 jaars swap.
De oorzaak van het probleem is gelegen in het niet adequaat specificeren van het renterisico. Een aanpassing op de traditioneel gebruikte MD blijkt nodig te zijn.
ALD: de juiste maat
Het ligt na het bovenstaande voor de hand het renterisico niet te specificeren als het risico op een verandering van het surplus, maar als het risico op een verandering van de dekkingsgraad.
Traditioneel wordt bij het berekenen van de afdekking gebruik gemaakt van de MD van de verplichtingen. Met behulp van deze MD, de waarde van de verplichtingen, en ook de waarde en MD van de beleggingen (incl. overlay) wordt dan het surplus afgedekt. Het surplus wordt berekend als het verschil van de waarde van beleggingen en verplichtingen. Dit heeft tot de traditionele gedachte geleid dat er een duration gap zou moeten worden afgedekt. Per abuis, zoals we hebben aangetoond.
De dekkingsgraad wordt namelijk berekend als het quotiënt van de waarde van beleggingen en verplichtingen. Intuïtief moge het duidelijk zijn dat de rentegevoeligheid van het verschil een andere grootheid zal zijn dan van het quotiënt. Met enig rekenwerk blijkt het mogelijk een aanpassing te vinden op de MD van de verplichtingen die een afdekking van de dekkingsgraad mogelijk maakt.
 De benodigde aanpassing op de MD van de verplichtingen blijkt eenvoudig een vermenigvuldiging met de dekkingsgraad te zijn:
De benodigde aanpassing op de MD van de verplichtingen blijkt eenvoudig een vermenigvuldiging met de dekkingsgraad te zijn:
ALD = dekkingsgraad * MD.
Door in plaats van met de MD van de verplichtingen met de ALD van de verplichtingen te werken, blijken we de dekkingsgraad nu wel af te kunnen dekken tegen renteveranderingen.
Hoe goed voldoet deze nieuw gevonden afdekking? Figuur 4 laat de dekkingsgraad zien als we wederom 100% afdekken met één 30-jaars receiver, waarvan we de notional amount nu gevonden hebben met behulp van de ALD.
Behoudens een zeer klein convexity effect is de dekkingsgraad vrijwel volledig afgedekt.
Ook voor de convexity berekenen we een verbeterde Adjusted Liability Convexity (ALC). Als het renterisico van de dekkingsgraad volledig is afgedekt blijkt dat:
ALC = dekkingsgraad * convexity.
NB als de dekkingsgraad niet volledig is afgedekt dan is deze aanpassing op de convexity niet bruikbaar. Opgemerkt zij dat het in de praktijk niet zal voorkomen dat een pensioenfonds wel haar convexity maar niet duration wil afdekken.
Wij hebben bovenstaande geïllustreerd met voorbeelden van volledige afdekking van de verplichtingen. Voor de gevallen van niet-volledige afdekking, laten we in Appendix 4 zien wat de relatie is tussen het afdekpercentage en de rentegevoeligheid van de dekkingsgraad.
Conclusie
In dit artikel bezien we of het afdekken van renterisico bij pensioenfondsen in de praktijk wel correct wordt berekend. De verwarring tussen het surplus en de dekkingsgraad van een pensioenfonds blijkt te leiden tot incorrecte afdekkingstrategieën. We tonen aan hoe schadelijk dit kan zijn voor het “afgedekte” pensioenfonds.
In toenemende mate gebruiken pensioenfondsen rentederivaten om het renterisico op hun balans te verminderen. In de analyses die zij hiertoe ontvangen worden de (modified) durations berekend van de beleggingen en de verplichtingen. Op basis hiervan wordt de ‘juiste’ afdekking berekend.
In de praktijk wordt aldus in veel gevallen het surplus van de balans afgedekt, terwijl juist de dekkingsgraad van het pensioenfonds veel bepalender is voor het beleid.
Met behulp van de hier beschreven Adjusted Liability Duration en Adjusted Liability Convexity wordt de dekkingsgraad van het pensioenfonds wel correct afgedekt tegen renterisico.
We hopen hiermee een bijdrage te leveren aan de kwaliteit van de markt van rente-afdekkingen – en aan het oplossen van de verbazing van pensioenbestuurders over onverklaarbaar gedaalde dekkingsgraden.
Appendix
1. Door Nederlandse pensioenfondsen wordt doorgaans de modified duration (MD) van de pensioenverplichtingen gebruikt om het renterisico te meten. Zoals bekend blijken aan de MD wel twee bezwaren te kleven, maar die kunnen worden opgelost. Ten eerste is de MD alleen bruikbaar voor kleine veranderingen in de rente. Voor grotere veranderingen kan de MD daarom samen met de convexity worden gebruikt.
Het tweede bezwaar is dat met MD alleen het risico van parallelle bewegingen van de rentetermijnstructuur wordt gemeten. Daarom berekent men veelal de afzonderlijke looptijdbuckets.
Als we een portefeuille met cashflows ct hebben met t = 0,...,T en als Z een serie zerocoupon rentes zt is, dan is de contante waarde C van de cashflows ct te berekenen als de som over alle tijdstippen t van ct / (1+ zt )t .
De gevoeligheid van C voor een verandering in een zt is d C/d zt = d ct /d zt = -t ct /(1+ zt )t+1, welke we de delta’s noemen, van t=0 tot en met T. De term delta (evenals de hieronder te bespreken gamma) ontlenen we uit de optiewereld. Deze delta’s zijn de eerste orde term in een Taylorreeks van C rond zt . Als we voor een 1 bp verandering van zt de hogere orde termen negeren dan is – vermenigvuldigd met 0.0001 – iedere delta een zerocoupon-PV01, namelijk de verandering van C voor een verandering van 1 bp in zt .
Door sommatie over de PV01’s van C naar alle zt vinden we C’ = d C/d Z. Dit is de PV01 voor een parallelle verandering van de rente curve van 1 bp.
Zoals bekend is de MD van de portefeuille gelijk aan -10000 * C’ / C. M.a.w. de PV01 en de MD zijn vergelijkbare grootheden op een schaling met -10000/C na.
Dezelfde afleiding kan worden gedaan voor de convexity. Hiervoor berekenen we eerst d2 C/d zt 2 = d2 ct/d zt 2 = ct t (t+1) /(1+ zt )t+2. Deze noemen we de gamma’s. De gamma’s zijn de tweede term in de Taylorreeks rond zt en vermenigvuldigd met 0.00012 zijn ze bruikbaar voor een 1bp verandering. Door weer te sommeren over alle zt vinden we C’’ = d2 C/d Z2 en de convexity van de portefeuille is (10000)2 C’’ / C.
Met L de waarde van de pensioenverplichtingen, A de waarde van de beleggingen, geldt dat het surplus S van een pensioenfonds gedefinieerd is als S = A – L. Het is onder pensioenfondsen gangbaar om het renterisico te beoordelen als het verschil in de rentegevoeligheid van beleggingen en verplichtingen. Er geldt S’ = A’ – L’, en voor 100% afdekking van het netto renterisico kan een afdekking D gevonden worden zo dat D’ =L’ – A’.
2. Soms wordt door pensioenfondsen de afdekambitie vastgesteld als een percentage van de verplichtingen. Formeel wordt een percentage x gekozen en wordt als doelstelling genomen om het renterisico van A – x L volledig af te dekken met een afdekking D (bv. een derivaten-overlay). Er geldt (x L)’ = x L’ en de afdekdoelstelling is daarom D’ = xL’ – A’.
3. We specificeren nu het renterisico niet als het risico op een verandering van het surplus, S = A – L, maar als het risico op een verandering van de dekkingsgraad, f = A / L. Nu is f’ = (L A’ – A L’)/ L2. Omdat voor een volledige afdekking geldt dat f’ = 0, geldt dat bij volledige afdekking A’ = f L’.
Anders uitgedrukt: als de beleggingen A niet leiden tot volledige afdekking zijn er andere rentedragende waarden D, bv. een derivatenoverlay, nodig met D’ = f L’ – A’.
Vergelijken we deze nieuwe voorwaarde, D’ = f L’ – A’, met de oorspronkelijke afdekkingvoorwaarde D’ = L’ – A’ dan zien we dat we in plaats van de MD van de verplichtingen we een adjusted liability duration (ALD) gebruiken. De aanpassing op de MD blijkt eenvoudig een vermenigvuldiging met f, de dekkingsgraad, te zijn:
ALD = f * MD.
Ook voor de convexity berekenen we een verbeterde Adjusted Liability Convexity (ALC). Er geldt dat f’’ = [ L2 (L A’’ – A L’’) – 2 (L A’ – A L’) L’ L] / L4 zodat als f’ = 0 en f’’ = 0 er moet gelden dat L A’’ – A L’’ = 0 ofwel A’’ = f L’’. Anders uitgedrukt wanneer we een derivatenoverlay zoeken die niet alleen voldoet aan de eis f’= 0 maar ook aan de eis dat f’’ = 0 dan moet naast D’ = f L’ – A’ ook gelden dat D’’ = f L’’ – A’’.
We kunnen tenslotte definiëren:
ALC = f * convexity.
NB als niet eerst als eis is gesteld dat f’ = 0 dan is deze aanpassing op de convexity niet bruikbaar. Opgemerkt zij dat het in de praktijk niet zal voorkomen dat een pensioenfonds wel haar convexity maar niet duration wil afdekken.
4. Als de afdekambitie vastgesteld is als een percentage van de verplichtingen, zagen we in Appendix 2 al dat de afdekdoelstelling dan A’ = xL’ is.
Zoals in Appendix 3 getoond is f’ = (L A’ – A L’) / L2, substitueren we hierin de afdekdoelstelling dan geldt f’ = [ L A’ – A (A’ + (1-x) L’) ] / L2 wat na enige herordening van de termen in de teller herschreven kan worden als f’ = (x L – A ) L’ / L2. Wegens L > 0 en L’ < 0 kan eenvoudig worden ingezien dat f’ een lineaire, dalende functie in x is.
Noten
- Dit artikel is door hen geschreven op persoonlijke titel.
- zie Appendix 1 voor de definities en afleidingen.
- Zie Appendix 2 voor een formele beschrijving van bovenstaande.
- zie Appendix 3
- zie Appendix 3
in VBA Journaal door Gijsbert de Lange (l) en Geert-Jan Troost (r)
