This article discusses the use of deflators for the valuation of financial contracts like insurance policies and pension plans. Many of such contracts contain option features. For example, several life insurance policies contain rate of return guarantees. Pension funds typically aim for full indexation of the benefits to price inflation, but in scenarios where inflation is extremely high or the funding ratio is low, indexation can be reduced or skipped altogether. These types of payouts are difficult to value with standard present value calculations, as it is not obvious which discount rate to use. However, the payout of the contract depends on some underlying variable like the stock price or the inflation rate. We can therefore see such contracts as contingent claims, or derivatives.
Starting with the path-breaking work of Black and Scholes (1973), a large literature on the valuation of derivatives has emerged. The key observation in the Black and Scholes analysis is that the derivative can be hedged by a position in the underlying instrument. The resulting cash position is risk free and therefore should earn the risk free interest rate. Working out this argument formally leads to the Risk Neutral Valuation (RNV) method.1 The RNV method calculates the price of the derivative as the expected payoff of the derivative in a risk neutral world, discounted at the risk free rate. In that risk neutral world, the expected return on the stock is set equal to the risk free rate. Risk Neutral Valuation is a very convenient and powerful method for the valuation of derivatives where the underlying value is a traded asset. It is less λ λε trivial to apply the method when the underlying determinant of the contingent claim is not a financial instrument, though. An important example of such a claim is an indexed pension benefit, whose payout depends on the price level or the inflation rate. The price level is not the price of a traded asset, so we cannot do as if the “return” on the price level equals the risk free rate. For such claims, a valuation method known as deflators is quite useful.
In this article I explain the concept of deflators by means of a few simple examples, starting with the stock price model of Black and Scholes (BS). I show how to construct a deflator for the BS model and how to use it to calculate the value of stock options. Then I turn to inflation contingent claims like pension contracts, and show how to construct a deflator for such claims.
The Black and Scholes deflator
Consider a simple one-period model (think of the period as one year). The price of the stock at the beginning of the period is S0, and the stochastic price at the end of the period is denoted by S. In the Black-Scholes model, stock prices follow a log-normal distribution. Formally, the returns on the stock are generated by
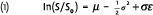
where ε is a standard normal random variable with mean zero and variance equal to one. The parameter µ equals the expected return, E[S/S0] = µ, and σ is the standard deviation of returns. A parameter that will play an important role in this article is the Sharpe ratio (or market price of risk) of the stock, defined as the risk premium (expected return minus the risk free rate, Rf ), divided by the standard deviation of the return
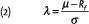
For the valuation of derivatives of the stock price, risk neutral valuation is the most common approach in the options literature, but here I present the valuation of derivatives using the deflator method.
The deflator is a stochastic discount factor, i.e. a discount factor that varies with the random variables driving the stock returns. The deflator takes the form
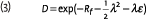
where ε is the random variable that defines the stock returns, and λ is the Sharpe ratio. For readers less familiar with continuous compounding, notice that this formula can be approximated (using a second order Taylor approximation) by
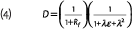
The deflator is the product of the risk free discount factor and a stochastic term, which depends on the shocks to the stock price.
The deflator can be used to calculate the value of derivatives of the stock price as follows. Denote the payoff of the derivative by X, which will be a function of the stock price at the end of the period X = f(S). The value of the derivative is then given by the expectation of the product of the deflator D and the payoff X:
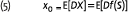
For an interpretation, let’s assume that the risk premium on the stocks is positive. The deflator then takes low values in states with a high stock return (high ε), and vice versa. One could also say that in states with low stock returns, the implicit discount rate for payoffs is low. Payoffs in “bad” states of the world, i.e. states where the stock price is low, will therefore have a relatively high value. Derivatives that mainly pay off in “bad” states of the world, such as put options, will therefore be relatively expensive compared to their (undeflated) expected payoff. On the other hand, assets that pay off when the stock returns are high, such as call options, will be less valuable.
We now discuss two important properties of the deflator. First, the deflator’s expectation is equal to the risk free discount rate. A riskless cash flow, say F dollars, will therefore be valued by the standard present value formula
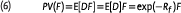
Another interesting special case is the stock itself. Working out the return equation (1) we find the stock price at the end of the year,
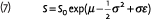
It is then easy to show that the deflated value of the end-of-period stock price equals the current price, E[DS] = S0. Another important example is a call option with exercise price K. The value of this option is given by
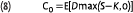
Working out this expectation can be done analytically, and will give the famous Black-Scholes option pricing formula.3 For less trivial payoffs, the expectation E[DX] can be approximated using Monte Carlo simulation.
An example
 We now turn to a simple numerical example for the valuation of options. Let µ = 9%, σ = 20% and Rf = 4%, so that λ = 0.25. We approximate the normal distribution of the stock return by a three-point distribution, where the random shock can take three values, +√2, 0, and –√2 with probabilities 1/4, 1/2, and 1/4 (with these numbers, the expectation is zero and the variance is one, as required). The stock returns and the deflator are given in table 1:
We now turn to a simple numerical example for the valuation of options. Let µ = 9%, σ = 20% and Rf = 4%, so that λ = 0.25. We approximate the normal distribution of the stock return by a three-point distribution, where the random shock can take three values, +√2, 0, and –√2 with probabilities 1/4, 1/2, and 1/4 (with these numbers, the expectation is zero and the variance is one, as required). The stock returns and the deflator are given in table 1:
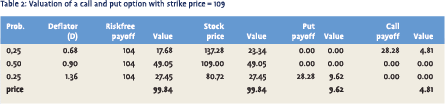 The last column in table 1 shows the implicit discount rate in each state, calculated as 1/D-1. In the state with the high stock return, the discount rate is 47%, but in state with low stock price the implicit discount rate is actually negative! Let’s now calculate the value of two options: a put option and a call option, each with strike X=109. Table 2 shows the payoffs of these options, and the value of each payoff (for each state, the “value” is defined as the payoff multiplied by the discount factor and the probability of that state):
The last column in table 1 shows the implicit discount rate in each state, calculated as 1/D-1. In the state with the high stock return, the discount rate is 47%, but in state with low stock price the implicit discount rate is actually negative! Let’s now calculate the value of two options: a put option and a call option, each with strike X=109. Table 2 shows the payoffs of these options, and the value of each payoff (for each state, the “value” is defined as the payoff multiplied by the discount factor and the probability of that state):
The put option paying off in “low” state is relatively valuable compared to the call with the same payoff in “high” state. Notice that the value of the stock and the risk free asset are (close to) 100, as they should be. The small difference is caused by the discretization error of using a three-point distribution.
Deflators for inflation-linked claims
We now turn to the construction of a deflator for price index (or inflation) linked claims. Although the price level or inflation are not assets traded on a financial market, one can use index linked bonds (ILB’s) to hedge claims that depend on changes in the price level. Specifically, let there be a (zero coupon) ILB, with notional value 1. The payoff of this bond is exp(π), where π is the inflation. Assume that inflation is stochastic with distribution
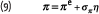
where πe is the expected inflation, assumed to be known in advance, and σπη is the unexpected inflation. The random shock η has a normal distribution with mean equal to zero and variance equal to one. The price of this bond at t=0 is equal to exp(-r) where r is the real interest rate, assumed to be known and constant. Hence, the nominal return on ILB is r + π, and its expected return ise + + π σπ 1 2 2
The market price of inflation risk is defined as the Sharpe ratio of the ILB return
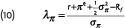
where Rf is the nominal risk free interest rate. The deflator is now defined in the same way as before
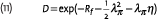
The valuation formula for inflation linked claims with payoff X = g(π) is
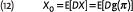
So far, this repeats the analysis of the Black-Scholes deflator, but with the Index Linked Bond (ILB) as the underlying asset. There is one crucial difference, though. Whereas it is natural to assume that stocks have a positive risk premium and hence a positive Sharpe ratio, the expected return on ILBs is quite low, and can be lower than the (nominal) risk free interest rate, i.e. 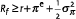 This will happen when investors are prepared to pay a premium to hedge against inflation risk. This will drive up prices of ILBs and hence give low real interest rates. The market price of inflation risk is therefore negative, λπ< 0. This means that payoffs in high inflation states will be relatively valuable, and payoffs in low inflation states are less valuable.
This will happen when investors are prepared to pay a premium to hedge against inflation risk. This will drive up prices of ILBs and hence give low real interest rates. The market price of inflation risk is therefore negative, λπ< 0. This means that payoffs in high inflation states will be relatively valuable, and payoffs in low inflation states are less valuable.
As an example, consider a pension fund with indexed liabilities, to be paid out 10 years from now. The real value of the liabilities is L=100, and the relevant interest rate and inflation parameters over the full 10-year period are r = 25%, πe = 20%, σπ = 20% and Rf = 50%. The inflation risk premium is 50 basis points (annualized), translating into a market price of inflation risk of 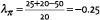
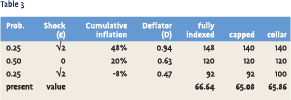 We calculate the value of three payout policies: one with full indexation and two limited indexation policies. In the first limited indexation policy, indexation is capped at 40%. In the second limited indexation policy, indexation is capped at 40% but there is also a nominal guarantee, so indexation is never negative. The table shows that these policies are One interesting result is that the third policy option, which limits the indexation in a symmetric way (20% above and below the expected inflation) is less valuable for the pension fund member than the full indexation. The reason is that the payoffs in the high inflation state are more valuable than the same payoffs in the low inflation state.
We calculate the value of three payout policies: one with full indexation and two limited indexation policies. In the first limited indexation policy, indexation is capped at 40%. In the second limited indexation policy, indexation is capped at 40% but there is also a nominal guarantee, so indexation is never negative. The table shows that these policies are One interesting result is that the third policy option, which limits the indexation in a symmetric way (20% above and below the expected inflation) is less valuable for the pension fund member than the full indexation. The reason is that the payoffs in the high inflation state are more valuable than the same payoffs in the low inflation state.
Extensions
In this paper, I discussed what deflators are and how they can be used for the valuation of contingent claims such as options and pension benefits. The paper discussed two specific examples, a deflator for stock price derivatives and a deflator for inflation contingent claims. A third important example are interest rate dependent claims, like portfolio’s of fixed income securities or the liabilities of insurance companies with embedded interest rate options.4 Two extensions of the examples are relevant in practice. First, the examples above construct the deflator from the Sharpe ratio of traded asset prices. For risks that are not traded on financial markets, one can still construct a deflator of the form
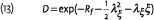
where ξ is the shock to the risk factor. The difference with the previous case is that the value of λξ cannot be derived from the expected return on traded assets, but has to be fixed exogenously.
A second extension of the examples is the valuation of more complex payoff structures that depend on multiple risk factors simultaneously. An example is a pension benefit that depends both on inflation and on the returns on the pension fund’s investments. It is possible, and actually quite easy, to build a deflator for multiple risks. Essentially, this can be done by multiplying the deflator for each individual risk factor.5 For example consider a payoff that is contingent on both the stock price and the inflation rate, X = h(S, π). The present value of this claim can be calculated as X0 = E[DsDπX], where Ds and Dπ are the deflators for stock contingent claims and inflation contingent claims, respectively.
Appendix: Monte Carlo simulation
The valuation of complex contingent claims cannot be done with analytical methods. Typically, Monte Carlo simulation is used. For the Black-Scholes deflator, this works in the following steps:
- Generate N values from the standard normal distribution, and calculate the associated values of the stock price
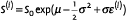 , the derivative payoff
, the derivative payoff 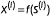 , and the deflator
, and the deflator 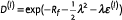 .
. - Average the deflated payoff of the derivative over all N simulations
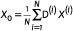
For many simulations (large values of N), this estimate converges to the true value of the contingent claim.
References
- Black, Fisher and Myron Scholes (1973), The pricing of options and corporate liabilities, Journal of Political Economy 81, 637-659.
- Brennan, Michael J. en Yihong Xia (2002), Dynamic asset allocation under inflation, Journal of Finance 57, 1201-1238.
- Cochrane, John H. (2001), Asset Pricing, Princeton University Press.
- Hull, John C. (2003), Options, Futures and Other Derivatives, fifth edition, Prentice Hall.
- Pelsser, Antoon (2003), Waardering van derivaten: risiconeutraal of deflators? De Actuaris, Januari 2003.
Notes
- This method is well explained for example in Hull (2003, Chapter 12).
- Essentially, the RNV and deflator methods are equivalent, and will give exactly prices of contingent claims. Only the way the calculations are done is different. See Pelsser (2003) for a good exposition of this point in a simple binomial pricing model.
- See Cochrane (2001, Section 17.2) for a complete derivation.
- Cochrane (2001, Chapter 19) gives an excellent treatment of deflators for interest rate contingent securities.
- This assumes the two risks are uncorrelated. For situations with correlated risk factors, see the analysis in Brennan and Xia(2002).
in VBA Journaal door Frank de Jong
