Over het waarderen en hedgen van garantieproducten
 Op woensdag 6 december 2000 komt een commissie bestaande uit leden van de Treasury, de Bank of England en de Financial Services Authority in spoedzitting in Londen bijeen. Deze commissie wordt alleen bijeengeroepen als zich gebeurtenissen voordoen die de financiële stabiliteit van het Verenigd Koninkrijk bedreigen. Die dag vernemen de leden dat Equitable Life, Engelands oudste onderlinge verzekeringsmaatschappij, gedoemd is ten onder te gaan. De ondergang van Equitable Life is te wijten aan een niet te controleren verlies van anderhalf miljard pond sterling op rentegarantieopties, de zogenaamde Guaranteed Annuity Options1 . Het verlies was te voorkomen geweest, als Equitable consequent de marktrisico’s van deze producten had afgedekt. Deze catastrofe roept de vraag op in hoeverre Nederlandse verzekeraars beschermd zijn tegen de risico’s van garantieproducten.
Op woensdag 6 december 2000 komt een commissie bestaande uit leden van de Treasury, de Bank of England en de Financial Services Authority in spoedzitting in Londen bijeen. Deze commissie wordt alleen bijeengeroepen als zich gebeurtenissen voordoen die de financiële stabiliteit van het Verenigd Koninkrijk bedreigen. Die dag vernemen de leden dat Equitable Life, Engelands oudste onderlinge verzekeringsmaatschappij, gedoemd is ten onder te gaan. De ondergang van Equitable Life is te wijten aan een niet te controleren verlies van anderhalf miljard pond sterling op rentegarantieopties, de zogenaamde Guaranteed Annuity Options1 . Het verlies was te voorkomen geweest, als Equitable consequent de marktrisico’s van deze producten had afgedekt. Deze catastrofe roept de vraag op in hoeverre Nederlandse verzekeraars beschermd zijn tegen de risico’s van garantieproducten.
Embedded opties
Een groot aantal producten van verzekeraars bevat garanties of embedded opties. Een goed voorbeeld hiervan is de minimum-rendementsgarantie (MRG), die vaak in combinatie met langlopende verzekeringsproducten wordt aangeboden. Zo’n polis met MRG biedt het beste van twee werelden: enerzijds profiteert de polishouder van de economisch goede jaren, anderzijds biedt de garantie de zekerheid dat waarde van de polis nooit onder een bepaald bedrag zal dalen.
Er bestaan nog tal van andere embedded opties, met name in verzekeringsproducten en hypotheken. In het verleden zijn de financiële waarde en risico’s hiervan vaak onvoldoende belicht. De reden hiervoor was dat de betreffende opties veelal “out of the money” waren (zodat de optie naar verwachting niet zou hoeven uitbetalen) op het moment dat de polis werd afgesloten. Impliciet veronderstelde men dat deze situatie in de toekomst niet zou veranderen. Garanties zijn daarvoor vaak zeer goedkoop of zelfs gratis weggegeven. Bovendien werden er geen voorzieningen voor aangehouden, laat staan dat de marktrisico’s van de garanties actief werden gehedged.
Sinds kort houden sommige verzekeraars in Nederland wel voorzieningen aan. Die zijn nog lang niet altijd gebaseerd op marktwaardewaardering2 en daardoor mogelijk niet groot genoeg. Belangrijk is dat risico’s nog niet actief worden gehedged. Slechts in de Verenigde Staten en bij enkele grote Europese verzekeraars worden de risico’s op juiste wijze ingeschat en afgedekt.
Waardering op marktwaarde heeft de toekomst
Tegenwoordig staan garantieproducten en embedded opties steeds meer in de belangstelling. Sterk dalende aandeelkoersen en renteniveaus hebben ertoe geleid dat de waarde van de garanties (en daarmee ook de verplichtingen voor de verzekeraar) zeer sterk is gestegen. De teloorgang van Equitable en problemen bij andere verzekeraars hebben de verzekeringswereld doen beseffen dat ongedekte garantieproducten een fenomenaal probleem kunnen vormen, dat zelfs kan leiden tot de ondergang van de eigen onderneming.
Er zijn nog andere redenen om garantieproducten onder de loep te nemen. We geven een kort overzicht. Regelgevers, accountants en credit rating agencies krijgen meer oog voor de waarde en risico’s van zowel assets als liabilities op marktwaarde. Voor garantieproducten betekent dit op termijn een marktconforme waardering. Op het gebied van regelgeving is binnen Europa overigens een opvallende tweedeling zichtbaar (Fulcher, 2002). In enkele landen – waaronder België, Duitsland, Zwitserland en Italië – staan de regelgevers nog sceptisch tegenover marktwaarde. In andere landen (met name het Verenigd Koninkrijk, Scandinavië en Nederland) neigen regelgevers juist sterk naar waardering en risicoberekening op basis van marktwaarde. De Pensioen- en Verzekeringskamer stelt expliciet in het Financiële Toetsingskader (FTK) voor 2005 dat opties op marktwaarde gewaardeerd dienen te worden. Binnen de accounting is tevens een duidelijke beweging gaande naar marktwaardewaardering. Dit blijkt uit de invoering van IAS/IFRS in 2005 (en voor verzekeraars deels in 2007). Het is nog niet geheel zeker of de nieuwe accountingregels de disclosure van garantieproducten op de balans tegen marktwaarde zullen eisen, maar gezien de huidige ontwikkelingen op het gebied van accounting lijkt dit slechts een kwestie van tijd. Tot slot spelen credit rating agencies een grote rol. Zij vragen steeds meer inzicht in de financiële positie van verzekeraars. Deze ontwikkelingen zullen er tezamen toe leiden dat verzekeraars in de toekomst anders tegen garantieproducten aan zullen kijken, dan in het verleden is gebeurd.
In dit artikel behandelen we verschillende praktische aspecten van garantieproducten. Aan de hand van een voorbeeldpolis laten we zien hoe de kosten van de garantie bepaald kunnen worden, en hoe hoog deze kosten typisch kunnen zijn. Nadat een polis is afgesloten, blijkt de marktwaarde van de garantie sterk gevoelig te zijn voor marktbewegingen. We tonen hoe groot deze gevoeligheid is en illustreren aan de hand van historische data dat de marktwaarde van de voorbeeldgarantie de laatste jaren is geëxplodeerd. De sterke waardeveranderingen maken duidelijk dat het identificeren en berekenen van risico’s alleen niet voldoende is. Daarom sluiten we dit artikel af met een praktische methode om de risico’s van embedded opties op een efficiënte manier af te dekken.
Waardering van een garantieoptie
De waarde van de rendementsgarantie kunnen we pas bepalen, nadat er een duidelijke scheiding is gemaakt tussen de garantie en het product waarin deze is ingebed. Die scheiding is voor de eenvoudige MRG producten niet moeilijk te maken. Neem aan dat een verzekeraar maandelijks premies ontvangt die, na aftrek van kosten, in een fonds worden belegd.
De verzekeraar verplicht zich na afloop van de polis het maximum uit te keren van twee bedragen, namelijk de opgebouwde waarde van de beleggingen (A) en het garantiebedrag (B). De beleggingen kunnen we als volgt scheiden van de garantie:
max (A,B) = A + max(B-A,0)
De schrijfwijze geeft duidelijk weer dat de uitbetaling van het product minimaal bestaat uit het opgebouwde belegd vermogen (A). Als het belegd vermogen tekort schiet en eindigt onder het gegarandeerde niveau (B), vult de garantieoptie het verschil aan.
Zo eenvoudig als de identificatie van de optie is, zo lastig is het om de waarde ervan te bepalen. De belangrijkste reden is dat de garantie geen standaard putoptie is. De payoff van de optie hangt namelijk niet alleen van de waarde van een fonds af, maar ook van een onzeker aantal participaties in het fonds. Iedere periode wordt de beschikbare premie belegd in het fonds. Aangezien de koers van het onderliggende fonds fluctueert, zal ook het gekochte aantal eenheden per periode verschillen. De garantieoptie is daardoor padafhankelijk en dat maakt een optie in het algemeen moeilijk te waarderen. Net als andere padafhankelijke opties kan de garantieoptie niet worden gesplitst in een serie losse opties.
Bij het waarderen van de garantie is het allereerst van belang dat men duidelijk voor ogen heeft waarover precies een garantie wordt gegeven. Wij kiezen ervoor de garantie te berekenen over de netto belegde premies. In sommige producten geldt de garantie voor de bruto premie, dus ook voor het deel dat niet belegd wordt maar door de verzekeraar als kosten wordt ingehouden. Dit komt in de praktijk neer op een verhoging van het daadwerkelijke gegarandeerde rendement op de beleggingen. De garantie wordt daarmee duurder.
Voor de waardering van de unit-linked garantie is helaas geen exacte gesloten uitdrukking beschikbaar (zoals de Black-Scholesformule voor standaard opties). De padafhankelijkheid maakt dat onmogelijk. Daarom worden alternatieve methoden gebruikt die we onder kunnen verdelen in de volgende categorieën: numerieke simulaties, analytische benaderingsformules of een recent verbeterde methode op basis van Laplace-transformaties.
Monte Carlo-simulatie wordt in de praktijk veel toegepast, maar een groot nadeel is dat de methode zeer rekenintensief is als men accurate resultaten wil verkrijgen. Snelheid blijkt de bottleneck, zeker als de waardering vaak herhaald moet worden (bijvoorbeeld als onderdeel van ALM-simulaties). In dat geval zijn analytische benaderingsmethoden (zoals de algoritmes van Levy en Curran) wellicht praktischer. Het grote voordeel van benaderingsmethoden is hun snelheid. Uit de literatuur is echter bekend dat de resultaten niet in alle omstandigheden even accuraat zijn.
Een interessant alternatief vormt de Laplace-transformatiemethode. Deze hybride methode is deels analytisch, deels numeriek. Hoewel de methode in de literatuur vaak als analytisch wordt aangeduid, hangt het succes ervan in de praktijk sterk samen met de kwaliteit van het numerieke inversiealgoritme. De nauwkeurigheid van dit algoritme is recent sterk verbeterd (Den Iseger en Oldenkamp, www.cardano-riskmanagement.com), zodat optiewaarden nu snel en accuraat kunnen worden berekend. Deze methode wordt met name aanbevolen in de gevallen dat snelheid een bottleneck is en er tevens grote nauwkeurigheid vereist wordt.
Bepaling van kosten voor de polishouder
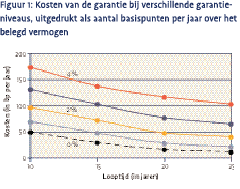 Om een concreet beeld te geven van de kosten van een garantieoptie voor de individuele polishouder, hebben we een voorbeeldpolis doorgerekend. Wij kiezen er hier voor de kosten van de garantie maandelijks te verrekenen als percentage van het belegde vermogen3. Het aantal basispunten is zodanig bepaald dat de contante waarde van de ingehouden fee naar verwachting gelijk is aan de marktwaarde van de optie.
Om een concreet beeld te geven van de kosten van een garantieoptie voor de individuele polishouder, hebben we een voorbeeldpolis doorgerekend. Wij kiezen er hier voor de kosten van de garantie maandelijks te verrekenen als percentage van het belegde vermogen3. Het aantal basispunten is zodanig bepaald dat de contante waarde van de ingehouden fee naar verwachting gelijk is aan de marktwaarde van de optie.
We kiezen als voorbeeld een polis waarbij maandelijks premies worden afgedragen. Het nettobedrag (duizend euro) wordt geïnvesteerd in een mixfonds dat voor 50% in aandelen en voor 50% in obligaties belegt. In de basissituatie gaan we uit van een rente èn een garantie van 4%. Voor het mixfonds gebruiken we een implied volatility van 14%, gebaseerd op de implied volatility van de onderliggende aandelenen obligatieindices en de correlaties daartussen. Andere effecten zoals overlijdensrisico of het premievrij maken van de polis laten we hier buiten beschouwing.
Voor een 10-jaars garantie met een gegarandeerd rendement van 4% vinden we een fee van ongeveer 175 basispunten van het belegd vermogen op jaarbasis. Zelfs bij een garantieniveau van 0% zou de fee nog altijd 50 basispunten op jaarbasis bedragen. Er valt duidelijk op dat het te verrekenen aantal basispunten afneemt bij toenemende looptijd. Dit geldt voor alle niveaus, maar de afname is relatief het sterkst voor de lage garantieniveaus.
Hier spelen enkele effecten door elkaar. Ten eerste wordt een optie in absolute zin duurder bij een langere looptijd, omdat er vaker premies worden gestort en het garantiebedrag hoger uitvalt. Maar kijken we vervolgens naar de kosten per periode, dan zien we juist een daling. Er worden vaker premies geïnd en het gemiddeld belegd vermogen valt naar verwachting hoger uit. Aangezien alle kosten relatief over het belegd vermogen worden berekend, kan per periode een kleiner aantal basispunten worden gerekend. Tot slot geldt: hoe lager het garantierendement (ten opzichte van de rente), hoe groter de kans dat de optie out of the money expireert. Daarom dalen de kosten van de optie relatief het sterkst bij lage garantieniveaus.
Dynamiek in marktwaarde: marktrisico’s
Vanzelfsprekend is de waarde van de garantie bij het afsluiten van de polis van belang, omdat de verzekeraar op dat moment kan bepalen welke kosten men wenst door te belasten. Maar een éénmalige kostenbepaling is niet voldoende. De marktwaarde van de optie zal in de loop van de tijd veranderen als gevolg van fluctuaties in fondswaarde, marktrente en implied volatility. Om te begrijpen welke implicaties die fluctuaties hebben op onder meer solvabiliteit en jaarresultaat is het van groot belang onderzoek te doen naar de gevoeligheid voor deze marktparameters.
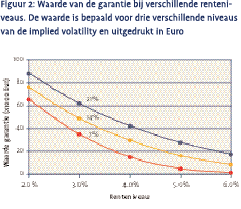 Figuur 2 toont de gevoeligheid van de waarde van de garantie voor de rente. De gevoeligheid van de marktwaarde van een optie voor de rente wordt aangeduid als rho4. We hebben de waarde berekend bij een looptijd van 25 jaar. De rente-effecten zijn bepaald door de rente te variëren van 2 tot 6%. Het garantieniveau is 4%. De drie curves in de figuur zijn ontstaan door de waarde te analyseren bij niveaus voor de implied volatility van 7, 14 en 21%.
Figuur 2 toont de gevoeligheid van de waarde van de garantie voor de rente. De gevoeligheid van de marktwaarde van een optie voor de rente wordt aangeduid als rho4. We hebben de waarde berekend bij een looptijd van 25 jaar. De rente-effecten zijn bepaald door de rente te variëren van 2 tot 6%. Het garantieniveau is 4%. De drie curves in de figuur zijn ontstaan door de waarde te analyseren bij niveaus voor de implied volatility van 7, 14 en 21%.
De gevoeligheid voor de rente is substantieel. Bij arbitrage-vrije waardering bepaalt de rente de verwachte toekomstige waarde van investeringen op de einddatum van de polis. Dit geldt zowel voor reeds belegde premies als voor toekomstige premiestortingen. Hoe lager de rente, hoe groter de kans dat de garantieoptie in the money eindigt en uit moet betalen. Anders gezegd: bij een lage (risicovrije) rente is de toegevoegde waarde van een rendementsgarantie het grootst.
Nemen we bijvoorbeeld het renteniveau van 4% (in de middelste curve), dan bedraagt de waarde van de garantie 29.000 euro. Bij een rentedaling van een procentpunt loopt de waarde op tot 49.000 euro, een relatieve stijging van 67%.
En passant geeft de figuur aan welke invloed de implied volatility heeft op de waarde van de garantie. De implied volatility is een maat voor de beweeglijkheid van het onderliggende fonds en in het algemeen geldt dat een hogere volatility leidt tot een hogere optiewaarde. De implied volatility is geen eenvoudig observeerbare marktparameter. Als het onderliggende fonds bestaat uit verschillende aandelen- of obligatie-indices, zijn bovendien de onderlinge implied correlaties nodig om de volatility te bepalen.
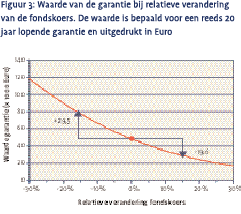 Een andere belangrijke marktparameter voor de waarde van de garantie is de koers van het onderliggende fonds. De gevoeligheid hiervoor wordt aangeduid met delta. Als de koers verandert, heeft dat alleen gevolgen voor de contante waarde van de reeds gestorte premies. De contante waarde van toekomstige premies wordt er niet door beïnvloed. Een belangrijk gevolg hiervan is dat delta uitgedrukt in Euro klein begint en groeit naarmate het aantal participaties in het fonds verder wordt opgebouwd. Het garantiefonds wordt in toenemende mate gevoelig voor de waarde van het onderliggende fonds.
Een andere belangrijke marktparameter voor de waarde van de garantie is de koers van het onderliggende fonds. De gevoeligheid hiervoor wordt aangeduid met delta. Als de koers verandert, heeft dat alleen gevolgen voor de contante waarde van de reeds gestorte premies. De contante waarde van toekomstige premies wordt er niet door beïnvloed. Een belangrijk gevolg hiervan is dat delta uitgedrukt in Euro klein begint en groeit naarmate het aantal participaties in het fonds verder wordt opgebouwd. Het garantiefonds wordt in toenemende mate gevoelig voor de waarde van het onderliggende fonds.
In figuur 3 tonen we de gevoeligheid van de voorbeeldpolis voor de marktwaarde van het onderliggende fonds. We bekijken de (at-the-money) optie nadat reeds 20 van de 25 jaar van de oorspronkelijke looptijd zijn verstreken, in plaats van op het moment van afsluiten. Op die manier wordt voorkomen dat het delta-effect wordt onderschat.
De convexe curve in figuur 3 is typerend voor opties. Een daling van de fondskoers leidt tot een stijging van de waarde van de garantie en vice versa, maar beide effecten zijn niet even sterk. Als de fonds 15% daalt, leidt dat tot een stijging van de waarde van de garantie met 30 duizend euro (en een navenant verlies voor de verzekeraar). Als de koers met eenzelfde percentage stijgt, is de winst voor de verzekeraar slechts 20 duizend euro. De koersgevoeligheid is niet-lineair.
Nu doen de garantieopties pijn
De laatste jaren is de markt geconfronteerd met een dalende rente, dalende aandeelkoersen en een stijgende implied volatility. Door het simultane effect is de waarde van garantieproducten geëxplodeerd en werden verzekeraars overrompeld door de kosten van hun embedded opties. Figuur 4 geeft hiervan een illustratie. Voor de figuur zijn we uitgegaan van dezelfde polis op het mixfonds waarvoor we eerder de kosten hebben berekend. De portefeuille bestaat louter uit gelijke polissen van garantieproducten met een oorspronkelijke looptijd van 15 jaar. De totale netto premie van de polissen bedraagt een miljoen euro per maand.
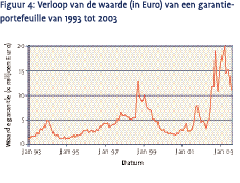 In de eerste jaren is een vrij stabiel waardeverloop zichtbaar. De eerste grote schok doet zich voor in de zomer van 1998: als gevolg van de Azië-crisis dalen de rente en aandelenkoersen. Het effect op de waarde van de garantie is duidelijk waarneembaar. Vervolgens keert de rust tijdelijk terug, tot aan de sluipkrach van de zomer van 2002. De optie is tegen die tijd zeer ver in the money geraakt en en reageert zeer sterk op het onderliggende fonds. Vervolgens zorgen gestaag dalende aandelenkoersen in combinatie met historisch lage renteniveaus ervoor dat de waarde van de garantie in korte tijd extreem oploopt: de waarde is in oktober 2002 vijf keer hoger dan een half jaar eerder. Op de top van de crash is de onafgedekte garantie 20 miljoen euro waard, tegen 1,1 miljoen euro op het moment van afsluiten.
In de eerste jaren is een vrij stabiel waardeverloop zichtbaar. De eerste grote schok doet zich voor in de zomer van 1998: als gevolg van de Azië-crisis dalen de rente en aandelenkoersen. Het effect op de waarde van de garantie is duidelijk waarneembaar. Vervolgens keert de rust tijdelijk terug, tot aan de sluipkrach van de zomer van 2002. De optie is tegen die tijd zeer ver in the money geraakt en en reageert zeer sterk op het onderliggende fonds. Vervolgens zorgen gestaag dalende aandelenkoersen in combinatie met historisch lage renteniveaus ervoor dat de waarde van de garantie in korte tijd extreem oploopt: de waarde is in oktober 2002 vijf keer hoger dan een half jaar eerder. Op de top van de crash is de onafgedekte garantie 20 miljoen euro waard, tegen 1,1 miljoen euro op het moment van afsluiten.
Uit bovenstaande analyse blijkt dat het voor prudent beheer van de solvabiliteit van de onderneming niet voldoende risico’s alleen te onderkennen. Een verveelvoudiging van de aanvankelijke waarde zou vragen om het aanhouden van extreem hoge voorzieningen of zeer veel kapitaal. Wil men efficiënter met kapitaal omgaan, dan moet men er voor kiezen de marktrisico’s actief af te dekken.
Hedgen van garantieproducten
In het geval van een perfecte hedge wordt het risicoprofiel van het garantieproduct exact nagebootst door een hedgeportefeuille van financiële instrumenten. Iedere waardeverandering van het garantieproduct wordt geneutraliseerd door een tegengestelde waardeverandering van de hedgeportefeuille. De combinatie van garantie- en hedgeportefeuille is op die manier ongevoelig voor veranderende marktomstandigheden.
In de praktijk kan een perfecte hedge niet, of alleen tegen zeer hoge kosten gerealiseerd worden. De lange looptijd van een garantieproduct – doorgaans 10 tot 30 jaar – en de ‘exotische’ structuur maken het tot een zeer illiquide product in de financiële markten.
Toch zijn goede hedgestrategieën wel degelijk mogelijk. Door gebruik te maken van liquide5 financiële instrumenten en regelmatig – bijvoorbeeld op jaarbasis – de hedgepositie bij te stellen, kan het marktrisico al aanzienlijk worden gereduceerd. Aanvullende randvoorwaarde voor de praktische haalbaarheid is dat de hedgestrategie effectief is bij de inzet van een beperkt aantal liquide producten. De rol van de afzonderlijke producten in de strategie moet helder zijn en eenvoudig kunnen worden toegelicht.
De gedachte achter iedere hedgestrategie is het neutraliseren van de marktgevoeligheden, in optietermen de Grieken geheten. Een hedgeportefeuille van opties, futures, swaps en swaptions wordt zodanig samengesteld dat de Grieken van de garantieportefeuille goed worden weerspiegeld. Het is niet eenvoudig in algemene termen aan te geven hoe vaak er gehedged moet worden, welke instrumenten er gebruikt moeten worden en wat de optimale looptijd van de hedgeinstrumenten is. De optimale hedge is namelijk toestandsafhankelijk. Zo is de garantieoptie naar het einde toe sterk afhankelijk van de koers van het onderliggende fonds, terwijl de rentegevoeligheid juist aan het begin van de looptijd het grootst is. Het is dan ook goed mogelijk dat in eerste instantie naast swaps en futures ook swaptions worden toegepast (om de rentegevoeligheid nauwkeurig af te dekken), terwijl in een later stadium opties naast futures worden gebruikt om de fondsgevoeligheid weg te nemen. Voor het bepalen van de optimale hedgefrequentie en -samenstelling heeft Cardano een waarderings- en risicoanalysemodel ontwikkeld.
Wanneer men ervoor kiest de langlopende opties te hedgen, zullen enkele bekende problemen moeten worden overwonnen. Voor het afdekken van de delta van een mixfonds is kennis nodig van implied correlaties, die notoir lastig te bepalen zijn. De rho is afhankelijk van een rentetermijnstructuur in plaats van een vlakke rente. Bovendien hangt de marktwaarde van de optie niet alleen af van de spot volatility maar ook van forward volatilities, waarvoor niet makkelijk hedgeinstrumenten kunnen worden gevonden.
 Als een hedge is aangebracht, zal er na verloop van tijd als gevolg van marktbewegingen een mismatch ontstaan tussen de risicoprofielen van de garantie en de hedgeportefeuille. Daarom moet de hedge periodiek worden bijgesteld. In de praktijk is een jaarlijkse aanpassing vaak al voldoende voor een goede risicoreductie. Behalve de periodieke bijstellingen kan ook een extreme marktgebeurtenis (zoals de Aziëcrisis of de sluipkrach van 2002) of nieuwe in- of uitstroom aanleiding zijn om de hedgeportefeuille aan te passen.
Als een hedge is aangebracht, zal er na verloop van tijd als gevolg van marktbewegingen een mismatch ontstaan tussen de risicoprofielen van de garantie en de hedgeportefeuille. Daarom moet de hedge periodiek worden bijgesteld. In de praktijk is een jaarlijkse aanpassing vaak al voldoende voor een goede risicoreductie. Behalve de periodieke bijstellingen kan ook een extreme marktgebeurtenis (zoals de Aziëcrisis of de sluipkrach van 2002) of nieuwe in- of uitstroom aanleiding zijn om de hedgeportefeuille aan te passen.
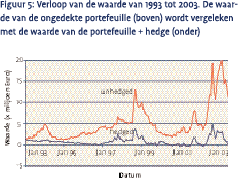
We bekijken nogmaals de resultaten van figuur 4. De initiële waarde van de garantieoptie bedroeg 1,1 miljoen euro. Had men vanaf het begin consequent alle marktrisico’s afgedekt, dan zou dat bedrag bij benadering hebben volstaan om de positie voor de totale looptijd dicht te zetten. In figuur 5 wordt het effect van hedging geïllustreerd. Jaarlijks wordt het bestaande marktrisico afgedekt, waarbij we voor de eenvoud slechts de lineaire risico’s hebben afgedekt. Het maximumverlies bedraagt nog slechts vijf miljoen euro, een reductie van 75% ten opzichte van de uitgangssituatie. Zou men ervoor kiezen de hedge verder te optimaliseren en ook niet-lineaire instrumenten (opties, swaptions) in te zetten, dan ligt een risicoreductie van meer dan 95% binnen bereik.
Conclusies
De wijze waarop verzekeraars met garantieproducten en embedded opties omgaan, zal de komende tijd sterk wijzigen. Zowel op het gebied van accounting als op het gebied van regelgeving voor verzekeraars is een duidelijke beweging merkbaar in de richting van marktwaardewaardering. Bovendien vragen credit rating agencies een steeds uitgebreider beeld van de financiële situatie van verzekeraars. Het debacle Equitable Life, dat door rentegaranties in faillissement is geraakt, en de recente explosieve waardestijging van tal van garantieproducten onderstrepen dat een andere aanpak gehanteerd moet worden dan tot voor kort gebruikelijk was.
1 Inzicht verkrijgen in de waarde van een garantie – In het verleden hebben verzekeraars embedded opties weggegeven, zonder dat men duidelijk voor ogen had wat daarvan de waarde was. Een polis met rendementsgarantie geeft de klant een putoptie die een financiële waarde vertegenwoordigt. Tegenwoordig kunnen we deze waarde met geavanceerde optiewaarderingsmethoden nauwkeurig bepalen. Op grond hiervan kan de verzekeraar ervoor kiezen de kosten marktconform aan de klanten door te belasten.
2 Voorzieningen bepalen op basis van marktwaarde – Wanneer men voorzieningen voor embedded opties aanhoudt, dient de hoogte ervan op marktwaarde gebaseerd te zijn. Alleen op die manier handelt men in lijn met de toekomstige regelgeving en accountingregels. Enkele verzekeraars bepalen hun voorzieningen voor garantieproducten reeds op marktwaarde.
3 Afdekken van marktrisico’s – Recente bewegingen van de financiële markten hebben laten zien dat een extreme waardestijging (een vertwintigvoudiging) van de waarde van de garantie tot de mogelijkheden behoort. Om dergelijke stijgingen op te vangen zou men ofwel extreem hoge reserves moeten treffen, ofwel zeer veel kapitaal aan moeten houden. Een efficiëntere manier om met kapitaal om te gaan, is het hedgen van de garantieproducten. Het blijkt goed mogelijk om een hedgestrategie te kiezen die praktisch uitvoerbaar en transparant is. De kosten van de hedgestrategie komen overeen met de waarde van de garantieoptie. Een substantieel deel van het marktrisico wordt al gereduceerd met een beperkt aantal zorgvuldig gekozen instrumenten, zodat de operationele belasting voor de verzekeraar beperkt blijft.
Het staat voor ons vast dat verzekeraars meer en meer zullen kiezen voor waardering op marktwaarde, doorbelasting van marktconforme kosten aan hun clienten en hedging van de marktrisico’s. We hopen dat deze keuze niet alleen wordt ingegeven door regelgevers, accountants en rating agencies, maar ook door het besef dat marktwaardewaardering de enige methode is om tot een marktconforme waarde van een optie te komen.
Referenties
- Bouwknegt, P. (2001) “De Ondergang van de Equitable”, De Actuaris (nov 2001)
- Curran, M. (1992) “Beyond Average Intelligence” Risk, juni 1992, p.60
- Fulcher, P, (2002) “Minimum Rate Guarantees Across Europe”, The Actuary, dec 2002
- Den Iseger, P. & E. Oldenkamp (2003), “Asian Options and Guaranteed Rate Products” (working paper), zie www.cardano-riskmanagement.com
- Levy, E. (1990) “Asian Arithmetic”, Risk, mei 1990, pp.7-8
- Lewis, P. (2001), “Trust is in the Balance”, The Guardian, 20 jan 2001
Noten
- De Guaranteed Annuity Option (GAO) is een rentegarantieoptie. De houder heeft het recht belegd vermogen om te zetten in een lijfrente tegen een gegarandeerd rentepercentage. GAO’s waren met name populair in het Verenigd Koninkrijk rond 1970-80. Equitable zegde garantiepercentages toe tot 8% in tijden dat de Britse lange-termijn rente ruim boven de 10% lag. Op het moment dat Equitable failliet ging, was de rente tot rond 5% gedaald. Zie (Bouwknegt).
- De grootte van de voorzieningen wordt soms nog gebaseerd op traditionele Embedded Value berekeningen. Deze methode is in het algemeen niet geschikt voor het meten van risico’s van embedded opties en garanties.
- Er zijn alternatieve manieren om de kosten te verrekenen, bijvoorbeeld door periodiek een percentage van de geïnvesteerde premie in te houden. Hoewel dit leidt tot andere kasstromen, zullen de verrekende kosten naar verwachting gelijk zijn.
- Rho is de gevoeligheid voor de zogenaamde financieringsrente van de optie. Een eventuele rentegevoeligheid van de onderliggende (met name in het geval van obligaties of obligatiefondsen) valt onder de definitie van delta. Rho is bepaald bij gelijkblijvende waarde van het onderliggende fonds.
- Bij het samenstellen van de hedgeportefeuille moet men een afweging maken omtrent de looptijd van de opties. Langlopende opties hebben als voordeel dat ze langer het profiel van de garantieportefeuille blijven matchen en dat ze relatief weinig tijdwaardeverval hebben. Anderzijds verslechtert de prijsvorming snel voor opties met een looptijd boven vijf jaar. In de OTC-markt zijn opties met een looptijd tot 5 à 10 jaar goed verhandelbaar.
Nawoord
Ik wil graag de drie anonieme referenten en mijn collega’s van Cardano Risk Management bedanken voor hun nuttige commentaar. Bijzondere dank gaat uit naar Jeroen van der Hoek van Cardano voor zijn grote steun bij het schrijven van dit artikel.
in VBA Journaal door Ir. Joeri Potters
