Inleiding
Een voorbeeld van succesvolle innovatie door Nederlandse beleggers is het gebruik van swaps en swaptions door pensioenfondsen en verzekeraars. Nadat deze Liability Driven Investors (LDI Beleggers, hierna beleggers genoemd) eerst swaps onder de knie hadden gekregen, zijn zij de afgelopen jaren ook swaptions gaan kopen om de renterisico’s van hun balans te beheersen. Hoewel de netto vermogens van vooral pensioenfondsen flink zijn aangetast, zou zonder deze derivaten de schade nog groter zijn geweest. Het gebruik door de beleggers van swaptions heeft goed gewerkt in de afgelopen drie jaren waarin eerst de rente fors daalde en daarna een aantal keren fors op en neer heeft bewogen. Doorgaans zien we echter dat vooral Nederlandse pensioenfondsen zich niet voldoende bewust zijn van de risico’s die de investering in deze derivaten met zich mee brengt.
 Meestal wordt de afweging swaptions of swaps te gebruiken namelijk alleen genomen op basis van de hoogte van de actuele rente: wordt deze als ‘laag’ beschouwd dan wordt een receiver swaption gekocht2 en als de rente ‘hoog’ gevonden wordt dan wordt een swap afgesloten. Bij renteniveaus ertussen in wordt dan een mix van swaptions en swaps afgesloten. De overweging is dat terwijl afdekking moet worden gevonden tegen een rentedaling, bij lage rentes de upside open gehouden moet worden.
Meestal wordt de afweging swaptions of swaps te gebruiken namelijk alleen genomen op basis van de hoogte van de actuele rente: wordt deze als ‘laag’ beschouwd dan wordt een receiver swaption gekocht2 en als de rente ‘hoog’ gevonden wordt dan wordt een swap afgesloten. Bij renteniveaus ertussen in wordt dan een mix van swaptions en swaps afgesloten. De overweging is dat terwijl afdekking moet worden gevonden tegen een rentedaling, bij lage rentes de upside open gehouden moet worden.
Van een stijgende rente moet worden geprofiteerd. Wat zal er echter gebeuren als de rente gedurende lange tijd constant blijft? In bijvoorbeeld een deflatoire economie is dit de realiteit en kan investeren in swaptions tot verlies leiden, terwijl de thans gebruikte beslismethode de beleggers telkens weer swaptions zal laten kopen. Het verlies is groter naarmate de voor de swaptions betaalde premie hoger is. Een alleen op absoluut renteniveau gebaseerde beslismethode moet worden uitgebreid en ook andere relevante marktfactoren beschouwen. De belegger dient ook over voor de hoogte van de premie relevante informatie te beschikken en deze mee te wegen in beslissingen. Voor de hoogte van de premie zijn de implied volatility en de steilte van de rentecurve belangrijk.
In het vervolg van dit artikel zullen we zien dat beleggers een aantal lessen kunnen leren van wat optiehandelaren in de praktijk doen. Deze lessen toepassend, gaan we de mogelijkheid nader bestuderen dat de keuze voor een swaption achteraf bezien ongunstig blijkt – achteraf spijt dus. We bespreken de relatie tussen de kans op spijt achteraf en de vooraf te betalen premie en introduceren een nieuwe indicator die op een betrekkelijk eenvoudige manier de relevante factoren samenbrengt en presenteert. Tenslotte zullen we zien hoe in de praktijk de signalen van deze indicator geïnterpreteerd kunnen worden en betere beslissingen over het gebruik van swaptions kunnen worden genomen.
Swaption spijt: de TW Range
Door alleen te denken in termen van stijgende rente of dalende rente wordt het risico van de gekochte swaptions zelf over het hoofd gezien. Elk financieel product heeft zijn eigen specifieke risico’s en bij het toevoegen van een product aan de portefeuille of balans worden bestaande risico’s getransformeerd tot nieuwe risico’s. Zo ook bij het afsluiten van swaptions, zoals aan de hand van het volgende voorbeeld duidelijk zal worden.
Laten we ons een belegger voorstellen die het risico op rentedaling heeft afgedekt met een gekochte receiver swaption. Als op de expiratiedatum van de swaption de rente voldoende is gedaald dan eindigt de swaption in-the-money. Is de rente echter gestegen dan eindigt de swaption out-of-the-money en is de belegger de betaalde premie kwijt, maar profiteert van de stijging van het netto vermogen door de gestegen rente. Als echter de rente ongeveer onveranderd is gebleven, dan is de belegger de premie kwijt en daalt het netto vermogen met het bedrag van de betaalde premie. Stel dat de belegger opnieuw een swaption koopt en dat de rente weer niet verandert. Voor de tweede keer daalt het netto vermogen met de betaalde premie. Zou zich dit blijven herhalen dan leidt het voortdurend tot verliezen voor onze belegger. Eenvoudigweg beslissen op basis van een ‘lage’ rente is dus een onvolledige en zelfs gevaarlijke strategie.
Optiehandelaren herkennen in dit voorbeeld meteen het risico van een long optiepositie in een markt die ‘stil zit’. ‘Stil zitten’ betekent dat de delivered volatility (de gerealiseerde volatiliteit) lager is dan de implied volatility waartegen de optie is gekocht. Onze belegger zal spijt hebben van zijn aangekochte swaption als de markt ‘stil zit’, spijt niet een swap te hebben afgesloten of het renterisico zelfs open te hebben gelaten. Door de aankoop van de swaption is het risico op een rentedaling getransformeerd naar het risico op een stilzittende rente.
Hoe stil mag de markt zitten of, andersom, hoeveel moet de markt juist bewegen? Het antwoord verschilt voor een dynamisch hedgende optiehandelaar en een belegger. Een optiehandelaar met een long optiepositie dekt zijn netto renterisico af en wil dat de rente beweegt, ongeacht op of neer. De handelaar varieert dynamisch de grootte van zijn hedges en maakt hier winst op doordat hij op lage niveaus koopt en op hoge niveaus verkoopt. De winst op het dynamische hedgen van het renterisico moet minstens het verlies van de premie goed maken. Als de markt stil zit dan maakt de optiehandelaar niet genoeg winst op zijn hedges en heeft hij achteraf spijt van de aankoop van de swaption.
Wij zullen nu nader de mogelijkheid bestuderen dat voor een belegger de keuze voor een swaption achteraf bezien ongunstig blijkt – achteraf spijt dus. Een belegger heeft twee alternatieven voor het afsluiten van een receiver swaption: het renterisico open laten, of het afdekken met een receiver swap3 . De hiervoor al genoemde spijt op het afsluiten van een swaption definiëren we in relatie tot deze twee alternatieven. De belegger is geïnteresseerd in de waarde van het netto vermogen op de expiratiedatum4 . We beoordelen de drie mogelijkheden aan de hand van de waarde van het netto vermogen, de Terminal Wealth (TW) op de expiratiedatum van de swaption. Hierbij gaan we ervan uit dat de belegger statisch hedged: tussen het afsluiten van de swaption en de expiratiedatum brengt hij geen veranderingen meer aan5 .
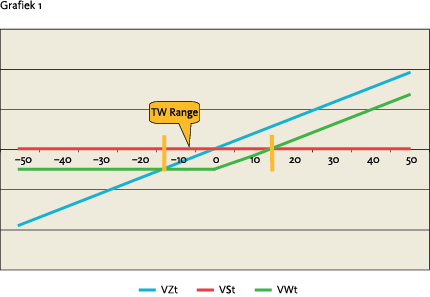 Zoals we hebben gezien, zal ook een belegger spijt hebben als achteraf de rente stil heeft gezeten. Voor de statisch hedgende belegger gaat het hierbij om het verschil tussen de rente op expiratiedatum en op de afsluitdatum. Om de huidige rente heen definiëren we een bovengrens en een ondergrens zo, dat als op de expiratiedatum de rente daarbinnen ligt de belegger spijt zal hebben van het afsluiten van de swaption: dit gebied zullen we de TW Range noemen. Ons doel is het minimaliseren van de kans op spijt. Voor een precieze afleiding van de TW Range verwijzen we naar de Appendix.
Zoals we hebben gezien, zal ook een belegger spijt hebben als achteraf de rente stil heeft gezeten. Voor de statisch hedgende belegger gaat het hierbij om het verschil tussen de rente op expiratiedatum en op de afsluitdatum. Om de huidige rente heen definiëren we een bovengrens en een ondergrens zo, dat als op de expiratiedatum de rente daarbinnen ligt de belegger spijt zal hebben van het afsluiten van de swaption: dit gebied zullen we de TW Range noemen. Ons doel is het minimaliseren van de kans op spijt. Voor een precieze afleiding van de TW Range verwijzen we naar de Appendix.
Grafiek 1 laat van ieder van de drie mogelijkheden het netto vermogen op de expiratiedatum zien bij verschillende renteniveaus. De x-as is gecentreerd rond de huidige rente. Bij hoge rentes is het netto vermogen met de swaption lager dan bij niet afdekken, maar hoger dan bij de swapafdekking. Bij lage rentes is dit omgekeerd, bij hoge en bij lage rentes is de swaptionafdekking een ‘goede tweede’. Het middengebied is de TW Range waar het netto vermogen met de swaption de laagste is van de drie en waar de belegger achteraf spijt heeft van het afsluiten van de swaption.
Breedte en positie van de TW Range – strike en optielooptijd
De TW Range doet denken aan de hoepel van een dompteur in een circusact: als de leeuw door de hoepel springt dan slaagt de act. Met de TW Range is het precies omgekeerd: als de rente op expiratiedatum in de TW Range eindigt dan ‘mislukt’ de swaption.
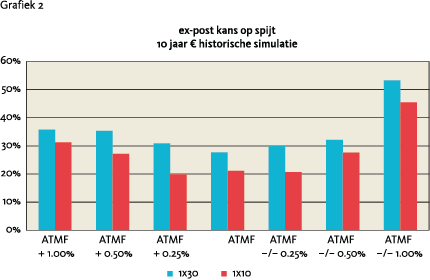 Hoe smaller de TW Range, hoe groter de kans dat de rente erboven of eronder zal eindigen en niet erin. Ook geldt dat hoe verder de TW Range van de huidige rente ligt, hoe kleiner de kans dat de rente erin zal eindigen6 . De afstand en de breedte van de TW Range worden beïnvloed door verschillende factoren, waarvan sommige door de belegger zelf gekozen kunnen worden, de andere zijn marktprijzen. In de Appendix wordt geanalyseerd hoe de keuze van de strike van invloed is op de afstand en op de breedte van de TW Range. Het blijkt dat een strike (ongeveer) gelijk aan de forward rente het gunstigst is. We hebben dit resultaat empirisch gecontroleerd door middel van historische simulatie. De dataset bestond uit EUR, USD en JPY swaprentes en At-The-Money-Forward (ATMF) swaptionvolatilities over de afgelopen 10 jaar. Voor de 3 valuta’s hebben we over de periode gekeken wat de ex-post kans op spijt was voor receiver swaptions met optielooptijden 1, 2 en 3 jaar en swaplooptijden van 10 en 30 jaar. Grafiek 2 toont de uitkomsten voor EUR 1x30 receiver swaptions en is representatief voor de gevonden resultaten. De ex-post kans op spijt was duidelijk het geringst voor strikes rond de forward7 .
Hoe smaller de TW Range, hoe groter de kans dat de rente erboven of eronder zal eindigen en niet erin. Ook geldt dat hoe verder de TW Range van de huidige rente ligt, hoe kleiner de kans dat de rente erin zal eindigen6 . De afstand en de breedte van de TW Range worden beïnvloed door verschillende factoren, waarvan sommige door de belegger zelf gekozen kunnen worden, de andere zijn marktprijzen. In de Appendix wordt geanalyseerd hoe de keuze van de strike van invloed is op de afstand en op de breedte van de TW Range. Het blijkt dat een strike (ongeveer) gelijk aan de forward rente het gunstigst is. We hebben dit resultaat empirisch gecontroleerd door middel van historische simulatie. De dataset bestond uit EUR, USD en JPY swaprentes en At-The-Money-Forward (ATMF) swaptionvolatilities over de afgelopen 10 jaar. Voor de 3 valuta’s hebben we over de periode gekeken wat de ex-post kans op spijt was voor receiver swaptions met optielooptijden 1, 2 en 3 jaar en swaplooptijden van 10 en 30 jaar. Grafiek 2 toont de uitkomsten voor EUR 1x30 receiver swaptions en is representatief voor de gevonden resultaten. De ex-post kans op spijt was duidelijk het geringst voor strikes rond de forward7 .
Minder duidelijk zijn de uitkomsten van de historische simulatie wanneer we kijken naar de invloed van de keuze van optielooptijd. Het is uit de berekeningen in de Appendix duidelijk dat de breedte van de TW Range groter is bij langere optielooptijden. Evenzeer neemt natuurlijk de range van mogelijke rentes toe bij langere looptijden. Het is daarom niet eenduidig wat de beste keuze van looptijd zou zijn. Uit de historische simulatie blijkt een lichte voorkeur voor 2 jaars looptijden. In de praktijk verdient het overigens ter vermijding van strike risk aanbeveling om looptijden te spreiden.
Opmerkelijk genoeg blijkt uit de simulatie ook dat veelal de ex-post kans op spijt groter was bij 30 jaars onderliggende dan bij 10 jaars. Als verklaring kunnen wij slechts speculeren dat de oorzaak misschien ligt in een imbalans tussen kopers en verkopers van swaptions op 30 jaars swaps waardoor swaptions op 30 jaars swaps relatief duur zijn.
Breedte en positie van de TW Range – implied volatility en curvesteilte
Terwijl strike, optielooptijd en swaplooptijd door de belegger zelf gekozen kunnen worden, zijn de implied volatility en curvesteilte door de markt bepaald. Hoewel een belegger op deze factoren zelf geen invloed heeft, is het wel van belang om bewust te zijn van de invloed van deze factoren op de afstand en breedte van de TW Range.
 In veel gevallen kan de belegger andere optiestrategieën kiezen die zijn risico op spijt reduceren of besluiten af te zien van swaptions en het risico open te laten of af te dekken met swaps. In de Appendix worden de gevoeligheden van de afstand en de breedte van de TW Range geanalyseerd voor deze marktprijzen. De conclusie is dat de bandbreedte toeneemt met toenemende implied volatility en/of curvesteilte.
In veel gevallen kan de belegger andere optiestrategieën kiezen die zijn risico op spijt reduceren of besluiten af te zien van swaptions en het risico open te laten of af te dekken met swaps. In de Appendix worden de gevoeligheden van de afstand en de breedte van de TW Range geanalyseerd voor deze marktprijzen. De conclusie is dat de bandbreedte toeneemt met toenemende implied volatility en/of curvesteilte.
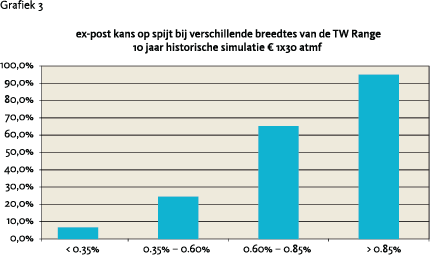
Een interessante vraag is of een grote breedte van de TW Range inderdaad leidt tot een hoge expost kans op spijt? Implied volatilities zijn slechte voorspellers van delivered volatility, net als forward rentes slechte voorspellers zijn van toekomstige rente. Ook uit onze simulatieresultaten kunnen we dit concluderen. Voor een 1x30 receiver swaption laat grafiek 3 zien dat de ex-post kans op spijt ruim boven de 50% was voor swaptions afgesloten wanneer de breedte van de TW Range groter dan 0.60% was. Onze indicator heeft dus een zeer goede voorspellende waarde voor de kans op spijt.
Swaptions in de praktijk
Wanneer de TW Range breed is en dus de ex-ante kans op spijt als hoog wordt geschat, verdient het aanbeveling te zoeken naar manieren om deze kans te verkleinen, zeker als de belegger zich een verlies van de premie niet kan veroorloven. Vooral willen we onderzoeken hoe het risico op implied vs delivered volatility verminderd kan worden. We kijken weer naar de praktijk van optiehandelaren. Liever dan outright optieposities op het boek te hebben, managen optiehandelaren hun risico’s door te spreaden: tegenover gekochte opties staan in hun boeken verkochte opties. Tegenover een long ATM put staat bijvoorbeeld een short put met een lagere strike: een put-spread. Op dezelfde manier kan een belegger die de TW Range van een ATMF receiver swaption te breed vindt er bijvoorbeeld een receiver swaption met lagere strike tegenover verkopen (een receiver spread) of een payer swaption met een hogere strike (een collar). Met spreads worden de risico’s weer op een andere manier getransformeerd: de TW range wordt smaller en het netto verlies aan premie geringer. Daar staat tegenover dat voor grotere rentebewegingen, voorbij de strike van de verkochte optie, het voordeel geringer wordt: bij een receiver-spread bij rentedaling en voor een collar bij rentestijging.
De TW Range is een indicator die het signaal kan geven om bijvoorbeeld spreads af te sluiten.
Vaak wordt door beleggers alleen het kopen van opties als conservatief beschouwd en worden short posities als te gevaarlijk beoordeeld. De bovengenoemde analyse laat duidelijk zien dat wanneer de TW Range indicator breed is, dit een schijnconservatisme is en de werkelijk conservatieve strategie door middel van spreading gevonden wordt.
Conclusie
De afgelopen jaren hebben Nederlandse verzekeraars en pensioenfondsen met succes swaps en swaptions ingezet om hun risico van neerwaartse rentebeweging af te dekken. Swaptions krijgen van deze beleggers de voorkeur als de rente als laag, respectievelijk. de mogelijkheid van een toekomstige rentestijging als groot wordt beoordeeld. Swaptions zijn echter geen panacea en brengen hun eigen risico’s mee: als op de expiratiedatum van een swaption de rente onvoldoende is veranderd dan leidt een swaption tot verlies. In dit artikel hebben we de TW Range geïntroduceerd als een indicator die het swaption risico eenvoudig en efficiënt weergeeft. Door de gevoeligheden van de TW Range te bestuderen voor strike, looptijden, implied volatility en curvesteilte en deze ook historisch te testen hebben we een aantal conclusies kunnen trekken. Voor beleggers zijn strike en looptijden zelf te kiezen en we hebben een aantal voorbeelden van goede keuzes laten zien. Vooral hoge implied volatility leidt tot een brede TW Range. Als deze te breed wordt, kan de belegger besluiten om af te zien van de aankoop van een swaption of om swaptionspreads af te sluiten.
Appendix
Afleiding van de TW Range
Definieer de volgende grootheden:
T – de expiratiedatum van een receiver swaption (jaar),
r0 – de huidige swaprente in de voor het renterisico relevante looptijd (%),
r T – swaprente op T in de voor het renterisico relevante looptijd en ∆ rT = rT – r0 (%),
fT 0 – huidige forward swaprente voor T (%),
k – strike van de swaption (%),
p0(k) – huidige premie voor receiver swaption met strike k (%),
AT – waarde van de assets op T en ∂ A / ∂ r = 0, AT = A0 (€),
LT – waarde van de verplichtingen op T (€) en ∂ L / ∂ r = ∂, LT = L0 + ∂ ∆ rT (€),
VT – vermogen op T en VT = AT + LT (€),
ST – waarde forward starting swap8 op T en ∂ S / ∂ r = –∂ voor notional N, S0 = 0, ST = –∂ (rT – fT 0) (€),
N – notional van de swap en van de swaption (€),
P0 – premie van de swaption en P0 = N p0(k) (€),
WT – waarde van de swaption positie op T, en W0 =0, WT = ∂ max(k – rT,0) – P0 (€)
Met behulp van deze notatie kunnen we voor de drie mogelijkheden het netto vermogen op de startdatum en op de expiratiedatum berekenen (hierbij is Vz T, Vs T en Vw T het netto vermogen resp. zonder afdekking, met swap afdekking en met swaption afdekking).
Op de startdatum geldt Vz 0 = Vs 0 = Vw 0 = A0 + L0 . Als we het renterisico open laten dan geldt voor het netto vermogen op de expiratiedatum: Vz T = A0 + L0 + ∂ ∆ rT.
Als we het renterisico afdekken met een forward start swap, dan geldt voor het netto vermogen op de expiratiedatum:
Vs T = A0 + L0 + ∂ ∆ rT – ∂ (rT – fT 0) = V0 + ∂ (fT 0 – r0).
Als we het renterisico afdekken met een receiver swaption, dan geldt voor het netto vermogen op de expiratiedatum:
Vw T = A0 + L0 – P0 + ∂ ∆ rT + ∂ max(k – rT,0).
Eenvoudig is in te zien dat bij hoge rentes (rT) geldt
dat Vz T > Vw T > Vs T, terwijl bij lage rentes (rT) geldt dat Vs T > Vw T > Vz T. Telkens is de swaptionafdekking een ‘goede tweede’. Er is een middengebied, de TW Range, waar we spijt hebben van het afsluiten van de swaption want er geldt Vs T > Vw T en Vz T > Vw T. Hier is de swaption variant telkens de slechtste van de drie. De grenzen (rT) van de TW Range leiden we als volgt af. Eerst bekijken we Vw T = Vz T. Hier geldt dat A0 + L0 – P0 + ∂ ∆ rt + ∂ max(k – rT,0) = A0 + L0 + ∂ ∆ rT ofwel P0 = ∂ max(k – rT,0).
We onderscheiden twee gevallen:
- k > rT: P0 = ∂ (k – rT) ofwel rT = k – P0 / ∂
- k <= rT: geen oplossing
Vervolgens bekijken we Vw T = Vs T. Hier geldt dat
A0 + L0 – P0 + ∂ ∆ rT + ∂ max(k – rT,0) = V0 + ∂ (fT 0 – r0) ofwel ∂ ∆ rT + ∂ max(k – rT,0) = P0 + ∂ (fT 0 – r0) ofwel rT + max(k – rT,0) = P0 / ∂ + fT 0
We onderscheiden weer twee gevallen:
- k > rT: geen oplossing
- k <= rT: hier vinden we rT = P0 / ∂ + fT 0
We hebben de volgende TW Range gevonden, waarbij we spijt van de swaption hebben als op de expiratiedatum: k – P0 / ∂ < rT < P0 / ∂ + fT 0 .
Centrum en breedte van de TW Range en hun delta en vega
Het centrum van de TW Range is (fT 0 + k)/2. De afstand van het centrum tot r0 is |(fT 0 + k)/2 – r0 | en neemt lineair toe met af- of toename van k. Het minimum wordt bereikt als k = 2 r0 – fT 0 . Als k = fT 0 wordt gekozen dan is de afstand precies | fT 0 – r0 |. Wat marktprijzen betreft is de afstand alleen gevoelig voor veranderingen in de rente (delta, gamma): hoe groter fT 0 – r0 , hoe groter de afstand. De delta en gamma van fT 0 zijn ongeveer 0 voor de meeste rentelooptijden langs de curve behalve voor looptijden T en T + 30 (de looptijd van de onderliggende swap). Het is eenvoudig in te zien dat bij een steiler wordende curve (tussen T en T + 30) de forward stijgt ten opzichte van de huidige rente. Voor een zo groot mogelijke afstand is de belegger dus gebaat bij een steile curve.
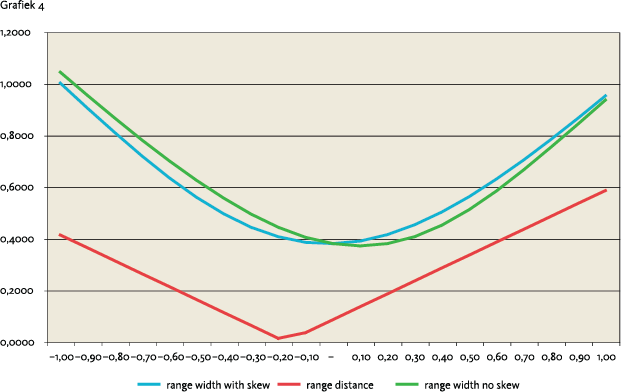 Grafiek 4 toont verschillende breedtes en afstanden van de TW Range bij verschillende strikes9 . Op de x-as staan de verschillende strikes, hoever deze onder en boven de forward rente liggen. De forward rente ligt in dit rekenvoorbeeld 9 bp boven de huidige rente. De schaal van de y-as is in %. De rode lijn toont voor verschillende strikes de afstand. De breedte wordt getoond door de groene (zonder implied volatility skew) en blauwe lijnen (met skew).
Grafiek 4 toont verschillende breedtes en afstanden van de TW Range bij verschillende strikes9 . Op de x-as staan de verschillende strikes, hoever deze onder en boven de forward rente liggen. De forward rente ligt in dit rekenvoorbeeld 9 bp boven de huidige rente. De schaal van de y-as is in %. De rode lijn toont voor verschillende strikes de afstand. De breedte wordt getoond door de groene (zonder implied volatility skew) en blauwe lijnen (met skew).
De breedte van de TW Range is precies 2 P0 / ∂ + fT 0 – k, waarbij de bovengrens P0 / ∂ + fT 0 – r0 boven de huidige rente ligt en de ondergrens er r0 – k + P0 / ∂ onder ligt. Het minimum wordt bereikt voor waarden van k vlak10 onder fT 0 als we een vlakke skew gebruiken. Bij een skew die verschilt per strike zal de gevoeligheid voor de implied volatility van invloed zijn. De breedte is gevoelig zowel voor veranderingen in de rente (bijna alleen van looptijd T en van T + 30) en voor veranderingen in de T x 30 swaption volatility behorende bij strike k. De delta van een receiver swaption is tegengesteld aan die van de forward rente. Afhankelijk van de keuze van de strike zal de rentegevoeligheid van de breedte hoogstens gelijk zijn aan de delta van 2 swaptions. Als k = fT 0 dan is de rentegevoeligheid gelijk aan de delta van 2 ATMF receiver swaptions (ongeveer -1) en wordt de breedte geringer bij een vlakkere curve. In dit geval is de delta van de breedte van tegengesteld teken en gelijk in grootte aan de delta van de afstand, bij een steilere curve wordt de afstand groter bij een (ongeveer) proportioneel grotere breedte. De invloed van curvesteilte is dus niet eenduidig. Voor grotere rentebewegingen verandert de delta van de breedte doordat er ook nog (positieve) gamma is. De gevoeligheid voor implied volatility van de breedte is gelijk aan 2 keer de vega van de receiver swaption. De TW Range wordt breder bij stijgende implied volatility.
Noten
- Dit artikel is geschreven op persoonlijke titel.
- Soms in combinatie met verkoop van een payer swaption.
- Of met een obligatie indien mogelijk. Zonder verlies van algemene geldigheid concentreren we ons in dit artikel op swaps omdat deze een zuivere vergelijking met swaptions mogelijk maken.
- Vanuit accounting oogpunt zijn beleggers ook geïnteresseerd in de marked-to-market bewegingen in de waarde van afgesloten swaptions tijdens hun looptijd. Dit geldt ook voor doorrol strategieën, waarbij voor expiratie doorgerold wordt.
- Deze 1-periode benadering kan eenvoudig worden gesommeerd over meerdere periodes om een multi-periode analyse te krijgen. Beantwoording van de vraag naar de optimale periodelengte van een swaption valt buiten het bestek van deze analyse.
- Aannemende dat de kans op een bepaalde grootte van renteverandering omgekeerd evenredig is met de verandering zelf. Dit is intuïtief duidelijk en ook het geval bij in de markt gangbare verdelingen (normaal, lognormaal).
- De historische simulatie is uitgevoerd met een vlakke skew, waardoor in EUR (waar lage strikes een hogere implied volatility hebben dan hoge strikes) de lage strikes er te gunstig uitkomen. Ook dient te worden bedacht dat in USD en EUR er gedurende de simulatieperiode een neerwaartse trend was van het renteniveau. Als we wel een skew zouden gebruiken en/of zouden corrigeren voor de trend dan zou in EUR de berekende ex-post kans op spijt voor lage strikes nog groter zijn.
- We gebruiken hier zonder verlies van algemene geldigheid een forward start swap, zodat we geen notatie hoeven in te voeren voor accruals. De aanpassing naar spot start swap is eenvoudig. Evenzeer hebben we een vereenvoudiging aangebracht door ∂ constant te veronderstellen.
- Voor deze grafiek hebben we 1x30 receiver swaption met een rentecurve van gemiddelde steilte en ATMF volatilities en skew van gemiddeld niveau gebruikt. Gemiddeldes zijn bepaald op basis van waarnemingen over de afgelopen 10 jaar.
- Ongeveer 0.5 tot 15 bp voor een 1x30 afhankelijk van de implied volatility, waarbij deze waardes gevonden worden door het minimum respectievelijk maximum te nemen over de afgelopen 10 jaar.
in VBA Journaal door Gijsbert de Lange (Towers Watson)
