Financiële instellingen kunnen niet zonder modellen. Modellen worden bijvoorbeeld gebruikt voor het vaststellen van de gewenste asset allocatie, het berekenen van (valuta) exposures en het waarderen van beleggingen. Modelrisico is het risico dat suboptimale of verkeerde besluitvorming plaatsvindt als gevolg van een onjuiste werking van een model of het gebruik van een verkeerd model, met financiële en/of reputatie impact als consequentie. Gebaseerd op zowel wetenschappelijk onderzoek als praktijkvoorbeelden, worden in dit artikel verschillende verschijningsvormen van modelrisico geanalyseerd. Daarnaast wordt door de auteurs ingegaan op de wijze waarop financiële instellingen dit risico effectief kunnen beheersen.
Manifestatie van modelrisico bij financiële instellingen
Het faillissement in 1998 van het hedge fonds Long Term Capital Management (LTCM) en de (model) risico impact die zich in 2010 bij Waddell & Reed heeft gemanifesteerd, tonen aan dat modelrisico kan leiden tot groot financieel verlies met zelfs een faillissement tot gevolg.
Het hedgefonds Long Term Capital Management (LTCM) hield zich in de jaren negentig bezig met relative value en convertible arbitragestrategieën. Om hoge rendementen te kunnen genereren was het voor LTCM noodzakelijk om beleggingen met veel geleend vermogen (leverage) te financieren. In 1998 had LTCM een balanspositie van 125 miljard dollar met slechts 5 miljard dollar aan eigen vermogen. Als de off balance posities zoals swaps, opties en andere derivaten werden meegenomen, ontstond een notional amount van 1.250 miljard dollar. Tijdens de Russische crisis en de Aziatische crisis eind jaren negentig, leed LTCM grote verliezen, omdat het fonds vanwege liquiditeitsproblemen niet in staat was om bestaande risicoposities te hedgen.
De situatie bij LTCM is voor een belangrijk deel ontstaan door het niet beheersen van modelrisico. Onderzoek van de Amerikaanse overheid (Report of the US President ‘s Working Group on Financial Markers, 1999) heeft aangetoond dat LTCM het belang van liquiditeit onvoldoende in haar risicomodel had verwerkt. Een onderzoek van Marthinsen (2009) heeft verder uitgewezen dat de parameters in het risicomodel van LTCM beter paste bij een zakenbank dan een hedgefonds. LTCM ging er bijvoorbeeld vanuit dat de rendementen van het hedgefonds volledig normaal verdeeld waren, wat in werkelijkheid niet het geval was.
Tevens bestond het beeld dat door prijsvolatiliteit eventuele prijsuitschieters snel zouden verdwijnen en het gedrag van individuele investeerders geen impact kon hebben op het geheel. Deze aannames bleken tijdens de Russische crisis niet langer stand te houden.
De ervaring van de Amerikaanse vermogensbeheerder Waddell & Reed op 6 mei 2010, is een ander voorbeeld van negatieve impact door modelrisico. Op die dag gaf Waddell & Reed om 13.32 uur via een computeralgoritme de order om voor ruim vier miljard dollar aan futures te verkopen. In de twintig navolgende minuten initieerde de computer de verkoop van 75.000 contracten op de markt. Het beurssentiment was ten tijde van deze verkoop uitgesproken negatief door de financieeleconomische situatie in Griekenland. Als gevolg van de grote transacties werden computeralgoritmes van high frequency traders getriggerd met de verkoop van futurescontracten als consequentie. Hierop reageerde vervolgens het computeralgoritme van Waddell & Reed Financial met nieuwe verkooptransacties. Op een gegeven moment wisselden op de markt 90.000 contracten per minuut van eigenaar, waarvan uiteindelijk slechts tweehonderd daadwerkelijk werden verkocht. Door de vele triggers in computeralgoritmes van verschillende investeerders, verloor de Dow Jones op deze middag negen procent van zijn waarde. Pas nadat het stabiliseringmechanisme op de futuresmarkt in werking trad en de handel vijf seconden lang werd stilgezet, normaliseerde de beurzen zich. Het computeralgoritme van Waddell & Reed hield geen rekening met de combinatie van een negatief beurssentiment en de uitvoering van grote future orders in korte tijd (zie Express.be, 2010 en Randal, januari 2010).
Bij zowel LTCM als Waddell & Reed waren modellen onvoldoende doordacht. Op basis van deze voorbeelden zou de conclusie getrokken kunnen worden dat modelrisico zich met name voordoet bij de implementatie van een model. Dit hoeft echter niet het geval te zijn. Het is ook mogelijk dat een ongeschikt model wordt gebruikt. Met andere woorden modelrisico kan gedefinieerd worden als het risico dat suboptimale of verkeerde besluitvorming plaatsvindt als gevolg van een onjuiste werking van een model of het gebruik van een verkeerd model, met financiële en/of reputatie impact als consequentie (zie voor meer informatie over definities van modelrisico: Derman, 1996).
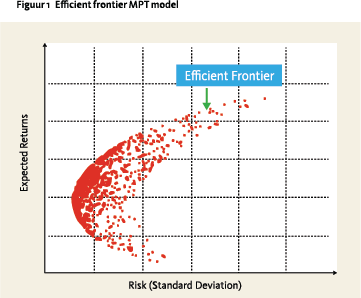 Het risico als gevolg van het gebruik van een verkeerd model manifesteert zich bijvoorbeeld indien een financiële instelling te rigide gebruik maakt van een model dat in de wetenschappelijk literatuur als normatief bekend staat. De moderne portefeuille theorie van Markowitz (MPT) is een voorbeeld van een normatieve theorie die door financiële instellingen te rigide als model gebruikt kan worden voor het vaststellen van hun beleggingsmix. Dit model stelt dat investeerders rationeel hun beleggingsmix vaststellen aan de hand van het verwachte rendement en de verwachte variantie, het portefeuillerisico. Bij de vaststelling van een optimale beleggingsmix voor een portefeuille bestaande uit aandelen, staatsobligaties en vastgoed, wordt conform het MPT model verschillende stappen ondernomen. Allereerst worden over een bepaalde periode de gemiddelde rendementen, varianties en de correlaties van de beleggingscategorieën geschat. Vervolgens wordt voor verschillende beleggingsmix-combinaties het verwachte rendement en het portefeuillerisico (variantie) gemeten en vervolgens grafisch geplot (zie figuur 1). Als dit voor alle mogelijke beleggingsmix combinaties is berekend, wordt aan de hand van een vooraf gestelde risicotolerantie de meest efficiënte beleggingsmix gekozen.
Het risico als gevolg van het gebruik van een verkeerd model manifesteert zich bijvoorbeeld indien een financiële instelling te rigide gebruik maakt van een model dat in de wetenschappelijk literatuur als normatief bekend staat. De moderne portefeuille theorie van Markowitz (MPT) is een voorbeeld van een normatieve theorie die door financiële instellingen te rigide als model gebruikt kan worden voor het vaststellen van hun beleggingsmix. Dit model stelt dat investeerders rationeel hun beleggingsmix vaststellen aan de hand van het verwachte rendement en de verwachte variantie, het portefeuillerisico. Bij de vaststelling van een optimale beleggingsmix voor een portefeuille bestaande uit aandelen, staatsobligaties en vastgoed, wordt conform het MPT model verschillende stappen ondernomen. Allereerst worden over een bepaalde periode de gemiddelde rendementen, varianties en de correlaties van de beleggingscategorieën geschat. Vervolgens wordt voor verschillende beleggingsmix-combinaties het verwachte rendement en het portefeuillerisico (variantie) gemeten en vervolgens grafisch geplot (zie figuur 1). Als dit voor alle mogelijke beleggingsmix combinaties is berekend, wordt aan de hand van een vooraf gestelde risicotolerantie de meest efficiënte beleggingsmix gekozen.
Indien een financiële instelling op basis van dit model haar beleggingsmix vaststelt, moet er rekening gehouden worden met het feit dat de MPT theorie een normatieve opzet kent, met aannames die in de praktijk vrijwel nooit van toepassing zijn. Het model gaat er bijvoorbeeld vanuit dat rendementen normaal verdeeld zijn en dat zonder problemen een objectieve risicotolerantie maatstaf vastgesteld kan worden, wat in werkelijkheid niet goed mogelijk is (zie Steenkamp, 2004).
Op basis van deze beperkingen kan de vraag worden gesteld of het MPT model in de praktijk wel geschikt is om een optimale beleggingsmix vast te stellen. De waarheid ligt waarschijnlijk ergens in het midden. Volledig steunen op het MPT model kan tot een suboptimale beleggingsmix leiden. Echter geen model hanteren en volledig steunen op gevoel is natuurlijk ook geen goed idee. De beste optie in deze situatie is om het MPT model te hanteren, maar kritisch te blijven op de uitkomsten van het model. Daarnaast is het raadzaam om naast de gebruikmaking van het MPT model, te steunen op inzichten uit bijvoorbeeld scenario studies, beschikbare wetenschappelijke literatuur en gezond verstand.
 Hoe kan modelrisico beheerst worden?
Hoe kan modelrisico beheerst worden?
LTCM, Waddell & Reed, en een rigide toepassing van de Moderne Portefeuille Theorie zijn drie voorbeelden waarbij sterk geleund wordt op modellen, maar waar minder aandacht is voor de negatieve effecten die het gebruik van dergelijke modellen met zich mee kan brengen.
Om modelrisico goed te kunnen beheersen is het belangrijk dat er binnen de organisatie aandacht bestaat voor het beheersen van dit risico. Indien er binnen de organisatie voldoende commitment aanwezig is, kan met behulp van een governance structuur de beheersing van modelrisico in een organisatie worden ingebed. De Federal Deposit Insurance Cooperation heeft in haar Supervisory Insights (Powel, 2005) gesteld dat een effectief governance framework begint bij het (senior) management. Het management is uiteindelijk verantwoordelijk voor het creëren van een cultuur waarin medewerkers bewust omgaan met risico’s, waar onder modelrisico. Daarnaast draagt een effectieve risk management en audit organisatie bij aan een betere beheersing van modelrisico (zie Board of Governers of the Federal Reserve System Office of the Comptroller of the Currency, 2011).
Het lijnmanagement, dat verantwoordelijk is voor de ontwikkeling van modellen en het gebruik ervan, moet er allereerst voor zorgen dat er effectieve controles worden ingericht om het modelrisico te mitigeren. Er kan bijvoorbeeld functiescheiding worden ingericht tussen enerzijds de modelbouwers en modelbeheerders en anderzijds de medewerkers die modellen valideren. Vorig jaar heeft onderzoek van Deloitte Consulting (2011) uitgewezen dat dit onderscheid in verantwoordelijkheden inmiddels gemeengoed in de financiële sector is geworden.
De risicomanagementfunctie is doorgaans (mede-) verantwoordelijk voor het identificeren, waarderen en beheersen van modelrisico’s. Door het regelmatig laten uitvoeren van een onafhankelijke modelvalidatie op nieuwe en bestaande modellen kan, in relatie met een effectieve governance structuur, worden voorkomen dat verkeerde modellen of onjuist geïmplementeerde modellen binnen een financiële instelling worden toegepast (zie Board of Governers of the Federal Reserve System Office of the Comptroller of the Currency, 2011).
De situatie bij LTCM was mogelijk niet uit de hand gelopen indien het risicomodel was onderworpen aan modelvalidatie. Indien bijvoorbeeld was getoetst in welke mate de rendementen van de hedgefondsstrategieën normaal verdeeld waren, was gebleken dat dit niet het geval was. Vervolgens had LTCM de aannames van het risicomodel kunnen aanpassen. Ook hadden gevoeligheidtoetsen, gericht op verschillende scenario’s, mogelijk tot waardevolle inzichten kunnen leiden, waarmee het model verbeterd had kunnen worden.
De Waddell & Reed casus had mogelijk voorkomen kunnen worden als er (meer) gevoeligheidtoetsen op het model waren toegepast. Indien het computeralgoritme was getoetst op basis van verschillende relevante scenario’s, zoals bijvoorbeeld de Azië crisis, dan had het model wellicht beter met dit soort marktsituaties om kunnen gaan. Daarnaast had mogelijke impact van high-frequency handelaren geanalyseerd kunnen worden in relatie tot de uitkomsten van het model. Back-testing was ook zinvol geweest, omdat een negatief beurssentiment vaak gepaard gaat met hoge handelsvolumes.
In de komende paragrafen wordt beschreven op welke manier modelvalidatie kan worden uitgevoerd. Modelvalidatie is een methode om vast te stellen dat het gebouwde model een juiste en volledige weergave vormt van de achterliggende theorie. Vanuit een methodologie perspectief wordt beschreven hoe de effectiviteit van een geïmplementeerd model getoetst kan worden. Daarnaast wordt vanuit een data en tooling perspectief aangegeven hoe de betrouwbaarheid van brondata en het onderliggende systeem kan worden geanalyseerd.
Methodologisch perspectief
Voordat een model gebruikt kan worden, is het van belang dat de methodologie van een model op effectiviteit wordt getoetst. Dit kan door bijvoorbeeld back testing en/of door gevoeligheidtoetsen toe te passen.
Back testing is een methode waarbij de effectiviteit van een model wordt getoetst aan de hand van historische data. Bij deze methodiek wordt historische data verzameld en vervolgens een selectie van deze data op het model toegepast. De uitkomsten van het model worden geëvalueerd door de resultaten van het model over langere tijd te meten. Door back testing over verschillende selectieperioden toe te passen, kan vastgesteld worden in hoeverre een model voldoet (zie Steenkamp, 2004)
Bij gevoeligheidtoetsen wordt op basis van historische data geanalyseerd hoe de verklarende variabelen van een model reageren op de verandering van andere variabelen. Gevoeligheidtoetsen kunnen op verschillende manieren worden toegepast. Het is mogelijk om de impact van een specifieke parameter te toetsen ten aanzien van de uitkomsten van het model. Met gevoeligheidtoetsen is het ook mogelijk om te analyseren welke parameters de meeste impact op de uitkomsten van een model hebben. Tenslotte kan met deze methodiek worden geanalyseerd hoe een model op verschillende scenario’s reageert. Bij een model voor asset allocatie kan bijvoorbeeld worden geanalyseerd hoe robuust de modeluitkomsten zijn voor een specifiek scenario. Door het uitvoeren van back testing of gevoeligheidtoetsen kan worden vastgesteld of het model de inzichten biedt, waarvoor het is opgezet (zie Grenville, 2007).
Naast back testing en/of gevoeligheidtoetsen kan het ook interessant zijn om het gebouwde model te benchmarken ten opzichte van modellen die bij andere, mogelijk vergelijkbare, organisaties gebruikt worden. Benchmarking kan hierbij enerzijds inzicht bieden in de mate waarin het model effectief is opgezet. Anderzijds kan de organisatie die deze benchmarking uitvoert, leren van de gemaakte keuzes die bij andere organisaties zijn gemaakt.
Dataperspectief
Bij een modelvalidatie is het belangrijk om vast te stellen wat voor data er in het model wordt toegepast. Er dient bijvoorbeeld onderscheid worden gemaakt tussen historische en prospectieve data. Dit is van belang, omdat het type data bepaalt wat voor soort validatie er uitgevoerd moet worden.
Indien een model gebruik maakt van historische data, dan zal de validatie in veel gevallen gericht zijn op de data infrastructuur en de beheersmaatregelen die zijn ingebouwd om de data-integriteit vast te stellen. Indien de validatie op een specifieke dataperiode is toegespitst, dan wordt de data integriteit wel in die specifieke periode vastgesteld, maar bestaat het risico dat de data in een latere periode niet betrouwbaar is (zie Mangiero, 2011)
Bij het opzetten van een dataset voor een model met prospectieve data zal bij de validatie goed geanalyseerd moeten worden of de data wel de juiste gegevens bevat en niet biased is.
Bij het analyseren van een beursindex door de tijd heen is het bijvoorbeeld van belang dat tussentijdse wijzigingen in de opzet van de index worden meegenomen. Als hierbij bijvoorbeeld geen rekening wordt gehouden met faillissementen die zich in de loop van de tijd hebben voorgedaan, dan vallen back-testing resultaten mogelijk positiever uit. Dit gegeven wordt in de literatuur ook wel “Survivorship bias”2 genoemd. (zie Ludwig et al, 2006).
Verder is het van belang om vast te stellen of eventuele vooronderstellingen over dataverdelingen overeenkomen met de werkelijkheid. Als bijvoorbeeld een VaR model wordt toegepast op data die niet normaal verdeeld is, bestaat het risico dat de resultaten van dit model niet betrouwbaar zijn. De asymmetrie van een verdeling kan vastgesteld worden door de scheefheid (skewness) en de piekvormigheid (kurtosis) van een dataverdeling te berekenen (zie Steenkamp, 2004).
Tooling perspectief
Bij de implementatie van een nieuw model moet de keuze worden gemaakt tussen het aankopen of het zelf ontwikkelen van een applicatie. Deze keuze heeft invloed op de modelrisico’s die een organisatie loopt.
Bij een applicatie van een softwareleverancier kan worden gesteund op ervaringen die in het verleden bij andere organisaties zijn opgedaan. Daarnaast kunnen dit soort applicaties structuur bieden, waardoor modellen op een meer eenduidige wijze worden geconfigureerd. Ingeregelde structuren kunnen wel tot gevolg hebben dat niet de gewenste mate van flexibiliteit kan worden geboden.
Ten slotte is de code van een extern gekochte applicatie over het algemeen een blackbox, waardoor het lastig is om software fouten vroegtijdig te detecteren en op te lossen.
Bij zelfgebouwde applicaties is het van belang dat modelbouwers zowel expertise hebben met betrekking tot het onderliggende model als ook de applicatie waarin het model wordt gebouwd. De meest accurate manier om modellen vanuit een tooling perspectief te valideren is, door elke calculatie afzonderlijk te controleren, eventueel ondersteund met speciale detectie software. De medewerker die het model valideert, kan er ook voor kiezen om het model zelf na te bouwen. Dit heeft echter als nadeel dat er ook in het nagebouwde model fouten kunnen voorkomen. Tenslotte kan ervoor gekozen worden om te volstaan met een plausibiliteitcontrole op de werking van het model. Het risico blijft dan bestaan dat niet alle fouten worden gedetecteerd (zie Grenville, 2007)
Conclusie
Een financiële instelling die negatieve impact als gevolg van modelrisico wil voorkomen, zal allereerst modelrisico moeten onderkennen als te beheersen risico. Binnen een in te richten governance structuur kan modelrisico worden geborgd. Deze borging is pas effectief als hiervoor organisatiebreed commitment bestaat. Met validatie technieken, kunnen modelrisico’s tijdig worden gedetecteerd. Instellingen die dergelijke beheersing niet toepassen, spelen Russisch roulette.
Referenties
- Board of Governors of the Federal Reserve System Office of the Comptroller of the Currency, (April 2011), Supervisory guidance on Model Risk Management
- Deloitte Consulting, (2011), Global Model Practice Survey, Report
- Derman Emanual, (1996), Model Risk, Goldman Sachs, Quantitative Strategies Research Notes
- Express.Be, (2010), De flash crash hoe een geautomatiseerde verkoop Wall Street deed beven, http://www.express.be/ business/nl/economy/de-flash-crash-hoen-geautomatiseerde-verkoop-wall-streetdeed-beven/133367.htm
- Grenville J. Croll, (2007), A typical model audit approach, Spreadsheet Audit Methodologies in the City of London
- Ludwig B., Chinacarini, Daehwan Kim, (2006), Quantitative Equity Portfolio Management, Mc Graw Hill
- Mangiero Susan, (2011), Financial model mistakes can cost millions of dollars, Expert Witnesses, Volume 7, Number 1
- Marthinsen, John, (2009), Risk Takers Uses of abuses of Financial Derivatives, Pearson, Prentice Hall, Second Edition
- Powel, Donald E., Spoth Christopher J., Fritts, (Winter 2005), Supervisory Insights, Volume 2, Issue 2
- Randal David, K, Flash Crash Report: Waddell & Reed’s $4.1 Billion Trade blamed for Market Plunge, (January 2010), http://www. huffingtonpost.com/2010/10/01/flash-crashreport-one-41_n_747215.html
- Report of the US President ‘s Working Group on Financial Markers, (April 1999), Hedge Funds, Leverage and the lessons of Long Term Capital Management, http://www.treasury. gov/resource-center/fin-mkts/Documents/ hedgfund.pdf
- Steenkamp, Tom, (2004), Asset Allocation and Portfolio Construction, Investment Service, Riskmatrix
Noten
- Drs. Kees-Jan van Vliet RBA, Risk Manager en drs. Klaas van der Meij, Principal Risk Manager, werken voor PGGM Vermogensbeheer B.V. Dit artikel is op persoonlijke titel geschreven.
- Door faillissementen, acquisities en beurs exits, zijn diverse ondernemingen niet meer in de (verouderde) dataset aanwezig, waardoor resultaten van Backtesting vertekend kunnen zijn. Zie voor meer informatie: Ludwig B, Chinacarini, Daehwan Kim, (2006), Quantitive Equity Portfolio Management, Mc Graw Hill, pagina 543.
in VBA Journaal door Kees-Jan van Vliet Klaas van der Meij
