Guidelines for Investment Corporations
 Introduction
Introduction
The purpose of any performance attribution system can be summarized in one phrase: creating and supplying transparent reports to target audiences. Unfortunately, defining the content of the reports is far from trivial; it depends on the investment process as well as the audience. For instance, trustees of pension plans are focused on main investment decisions. They want a one-page summary report that clearly shows them how much money was gained or lost on the strategic, tactical, and operation levels. On the other hand, portfolio managers need highly detailed information on the performance of all securities in their portfolios. In this context, consistency is a complicated factor. Ideally, there are detailed attribution reports for all investment categories that add up to one overall attribution report, without any residual. But how do we achieve that? How should one integrate the currency overlay program? How can we link specific fixed income attribution results to the summary report?
The calculation methodology adds more complexity to the problem. Reporting on time-weighted returns might be fair to portfolio managers, but is it also fair to investors? Is there a true need to turn to geometric excess returns, or are we just considering it because it is widely accepted? Is the more intuitive arithmetic excess return not just as good?
In this paper we provide guidelines for setting up a performance attribution framework that deals with these issues. The first step in the framework is drawing up the investment structure. This should be the core of the attribution analysis. Next, one has to fix the evaluation periods. These periods should match the frequency by which investment decisions are actually made. Thirdly, all cash flows need to be identified; the challenge is to capture the implicit flows. The fourth step is the calculation of returns. Surprisingly perhaps, this is not a trivial step. Especially when we incorporate the currency dimension as we do in step 5. Step 6 is another non-trivial step: calculating excess returns. The final step in our framework is the choice of attribution scheme. There are many options and there is no single model to fit all needs. Key in our approach is the investment process. All steps in the framework fall back on this process, while we work our way down to the actual formulas. This is quite different from the approach used by many performance professionals. They first select an attribution method and then try to squeeze this method into the investment organization.
Setting up the framework
In this section we describe the seven steps to set up a performance attribution framework.
Step 1: Define the Investment Process
In our framework, the first step is the most important. A performance attribution report only gives useful information if it is based on the investment decision process (IDP). Every investment decision should be acknowledged in the attribution. This is the only way to assure that the overall profit or loss is completely accounted for. On the other hand, it is almost equally important not to overrate the number of investment decisions. This will lead to spurious results that the investment team cannot account for.
Step 2: Determine the Unitization Period
The next step is the choice of the evaluation period, also called unitization. Is this relevant? We certainly believe so. The choice of the evaluation period in the return calculations is often dictated by practical limitations. This is unfortunate, because it is a persistent misunderstanding that, even in the absence on intra-month trades, compounding daily attribution effects to month is identical to a monthly attribution. If you do the numbers, you will immediately see that this is not the case. Yet, one cannot state simply that daily attribution is superior to monthly, or vice-versa. We believe that the evaluation period should mimic the frequency by which investment managers are updating their strategy2. For a global TAA team this frequency might be monthly, while a fund manager may revalue his positions every day.
Step 3: Model all Cash Flows
We believe a correct understanding of cash flows is crucial for obtaining a consistent framework. Explicit cash flows – such as injections & withdrawals, portfolio rebalancing, and transactions – are not subject to discussion. But, we are also interested in the implicit flows that are typically induced by the investment structure. For example, when a fixed income manager is not responsible for currency risk, conceptually this risk is transferred to another part of the process. When this flow is neglected, the currency exposure is a possible source for unexplained – and hence unattended – risk and return.
Step 4: Turn to Returns
Returns are commonplace, yet they can be a major source of confusion. In its bare essence, a return is a profit or loss related to some performance base. It is the performance base that makes return calculations complex. Since returns are a starting point for the performance attribution, you might run into troubles. You should take care in choosing an appropriate performance base. As an example we look at the difference between time-weighted returns (TWR), modified Dietz returns (MDR), and internal rate of return (IRR).
- TWR The TWR filters the effects of transactions. A return is calculated from transaction to transaction. These returns are chain linked to obtain returns over longer periods. This means a return-on-return effect is present. It is a misunderstanding that a TWR is not useable for attributions. The argument used is that TWR removes the cash flow effect. But in fact it only removes the effect of cash flows within a segment, not over segments. Hence, overand underweighting of segments is still correctly measured.
- MDR The MDR does incorporate cash flows. It relates the profit or loss in a certain period to a performance base. This performance base is equal to the market value at the beginning of the period plus the timeweighted cash flows during the period. MDR ignores return-on-return effects. This implies that in a two-year report the realized gain of year one is not subject to market movements in year two. MDR suffers from a fading effect; the return of a terminated portfolio tends to zero over time. The main limitation of the MDR is that it is only allowed to compare two portfolios when they have been subject to the same cash flows. It is often forgotten that the benchmark is therefore also subject to cash flows.
- IRR The IRR is usually interpreted as a truly money weighted return. The interpretation of this return is not always intuitive. You could state that “whenever a bank offers you an interest rate for the whole period that is more than the IRR, you should put your money on the bank”. Since the IRR is defined as the root of a polynomial, a rootfinding algorithm is required to obtain the IRR. That makes it hard to calculate this return. Furthermore, IRR does not add up over portfolios, i.e. weighting the IRR of two portfolios and summing them up is not equal to the IRR of the two portfolios together. IRR has the same fading effect as the MDR.
There is a growing appeal to use money-weighted returns in reporting to clients. Money weighted returns better reflect the actual profit/loss of the client than time weighted returns. This might be true, but it is often forgotten that in that case benchmarks should be subject to the same cash flows as the portfolio. Otherwise, you simply cannot compare the portfolio to the benchmark return. If you fail to do so, cash flow effects are assigned to the selection (& interaction) effect. This implies that in case of an entirely passive portfolio a surprising selection effect pops up. Nonetheless, there is a major disadvantage of taking cash flows into consideration in benchmark returns. You will end up with different returns for the same benchmark; the benchmark return depends on the portfolio you are comparing it to.
Step 5: Address the Currency Dimension
In an international investment portfolio, currency management is an important aspect. Basically there are four ways to include the currency effect in the return calculations:
- Local returns: Ignore all currency and interest components;
- Unhedged returns: Convert all returns to a single base currency;
- Hedged returns: Remove the currency surprise effect; only consider interest rate differentials;
- Risk premiums: Consider the difference between the local return and the risk free rate.
The choice for one of the above return definitions should be based on the investment process. When currency management is integrated in the portfolio investment strategy, unhedged returns are usually reported. In the case of an overlay program, the returns used for attribution are either hedged (Fully Hedged method [6]) or based on risk premiums (Singer and Karnosky [9]). The local return is sometimes used when managers are not responsible for currency movements. However, this is not recommended, since local returns are not comparable. It is possible that different return definitions apply to different parts of the investment process. However, remember that on an overall level the methodology must be consistent. This means that effects that are taken out of one part of the process, should reappear in another part.
Step 6: Calculate Excess Returns
Once portfolio and benchmark returns have been defined, we can start thinking about excess returns. At this stage of the process, the duality of the benchmark arises. On one hand, benchmarks are a proxy of returns experienced by the average investor. On the other hand, the benchmark acts as an alternative or reference portfolio. The difference between the two is the treatment of cash flows. When defining excess return and selecting an attribution methodology, we have to make a choice between the two concepts. The arithmetic excess return is defined as the portfolio return minus the benchmark return:
Rpf – Rbm
This excess return uses the concept that a benchmark is nothing else than a measure of average market return. At the beginning of each period, you give the same bag of money to the portfolio manager as the ‘average’ investor. At the end of the period you collect the bags and evaluate who did best. Wellknown arguments in favor of using arithmetic excess returns are:
- Arithmetic excess returns are easy to understand, and
- They are widely used.
The first argument is a valid argument. Intuitively, people deduct numbers when you ask them how a portfolio performed in comparison to some benchmark return. The second argument is of course not very strong; it is probably a consequence of the first argument.
The geometric excess is defined in the following way:
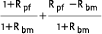
This methodology divides the arithmetic excess return by the wealth ratio. By wealth ration we mean the ending market value of the benchmark portfolio. As a result the excess gain or loss is expressed in terms of the terminal value of the alternative portfolio, i.e. the opportunity wealth. Much-heard arguments in favor of using geometric excess return are:
- Compoundable; i.e. the excess return can be linked over time;
- Proportionate; i.e. the excess return is scaled by market movements;
- Convertible; i.e. the excess return is the same in any (reporting) currency.
The first argument is to some extent a matter of taste. Why should it be an advantage that you can compound an excess return? One reason could be that it is consistent with viewing the benchmark as an alternative portfolio. Another could be that, when estimating a monthly excess return, the sum of thirty daily geometric excess returns is by far a more accurate approximation than the sum of thirty daily arithmetic excess returns. This is a hidden argument that we could call predictability.
Clearly, the second argument is valid only if you attach value to it. Is it more impressive to obtain an excess return of 1% in a bear market than in a bull market? If so, it makes sense to scale the excess return with the average market movement.
We believe that convertibility is a special case of proportionality. Currency movements are also market movements, so it is not surprising that a geometric excess return annihilates the currency effect.
Finally, we give two arguments that are expressed every now and then. But in fact, they can never be used as an advantage for either of these methods:
- “My method provides better interpretation in terms of money alpha”. This is simply not true. Cash flows obscure this interpretation in both methodologies;
- “Your method is only a first order approximation of my method”. Taylor expansions are symmetric, so if f(x) = g(x) + o(xn) then also g(x) = f(x) + o(xn).
Concluding, both the arithmetic and geometric definition have their pros and cons. It is really a matter of taste which method you choose.
Step 7: Choose the Appropriate Attribution Scheme
In the previous steps you have established, in broad terms, which attribution schemes are appropriate. In this section, we will summarize the options by asking ourselves four questions.
On which (aggregated) portfolios would I like to perform an attribution, and what is the appropriate segmentation?
Once you have defined your investment process in the first step, the answer should be clear. The investment structure sets down a hierarchical process that is made up of summary levels. Hence, the segments on each aggregation level are its direct ‘children’. Apart from the formal investment process, portfolio managers might benefit from additional portfolio breakdowns, e.g. from portfolio to sector, credit class or stocks.
 Which effects would you like to see?
Which effects would you like to see?
The effects in any attribution method reflect the investment decision. The decisions made by managers of fixed income portfolios differ from those of equity or overlay portfolio managers. This has consequences for the attribution methodology. Besides, we have to decide how to deal with currency effects. Is it appropriate to separate the currency effect or split it into an expected and currency surprise effect? Also, we need to look at the investment structure to determine the order in which decisions are made. The most widely used attribution models distinguish allocation, selection, and interaction effects. Depending on the hierarchy of the decisions, these effects are summed in the following way:
- In a top-down approach, the selection decision follows the allocation. This implies that first segment weights are set, before there is (stock) selection in each segment. In this case the interaction term is added to the selection term;
- In a bottom-up approach the first decision is stock selection. Subsequently, tactical managers can over- or under-weight segments by applying an overlay strategy. In this case the interaction is added to the allocation effect;
- In a simultaneous approach the allocation and selection decisions are made at the same time. In this case the interaction effect should be reported separately.
There have been many discussions on the meaning of the interaction effect. Technically, it is the effect that arises when you simultaneously allocate to and select in a segment. Functionally, overweighting a segment in which you pick the right stocks leads to a positive interaction effect. The other way round, underweighting a segment where you pick less performing stocks, results in a negative allocation effect. When the interaction term dominates the other effect there is something wrong with the allocation and/or selection. Or, alternatively, the benchmark does not resemble the portfolio enough. In this case, one should ask oneself whether the investment process is appropriate. Geometric attribution schemes usually imply a simultaneous approach because of the multiplication, but it is possible to define an interaction effect explicitly.
Which methodology do you want to use?
The elementary choice is whether you use the Brinson-Hood-Beebower (BHB, see [2]) or the BrinsonFachler (BF, see [3]) concept. BHB labels an allocation as positive when the manager has over-weighted a segment yielding a positive benchmark return. On the other hand, BF only regards this decision successful when the over-weighted segment’s benchmark performs better than ‘average’. Were average is defined as the overall benchmark. The reasoning of BF is that overweighting one segment automatically results in underweighting one or more other segments and vice versa.
It is commonly acknowledged that BF is superior to BHB. However, situations where you definitely should prefer BHB are overlay programs. Indeed, why should the hedge of USD have impact on the amount you are allowed to hedge from JPY? A less clear situation where you might consider BHB is when you use risk premium as returns. In fact, the use of risk premiums implies a budget-neutral situation; you borrow the money to invest. Hence, overweighting one segment no longer implies underweighting another segment. In this section we focus on single period attribution methods. The figure shows how segments and effects are aggregated. Arithmetic attributions are quite straightforward since they always sum up, both over segments and effects. In a geometric setting there might be a residual within a single period. A residual means that the attribution effects do not fully explain the excess return. This happens in the figure on the right, where segments results are compounded. While Allen (see [1]) simply accepts the residue, Menchero (see [8]) distributes the residue over the other effects.
How do you deal with multi period attribution?
Similarly to returns, attribution effects can be linked over time. In an arithmetic setting a problem might arise. The chain-linked effects might not fully explain the excess return over the same period. More precisely, chain linking of summed effects is not equal to summing chain-linked effects. To overcome this problem, various smoothing algorithms have been proposed (see Cariño [5], Menchero [7]). However, if you cannot avoid a residue, you might as well consider showing it.
Conclusions
In this paper we described a step-by-step approach to set up a performance attribution framework. An appropriate performance attribution mirrors the actual investment decision process (IDP). Therefore we advocate using the IDP as your starting point. In this way the management structure of the investment organization is the basis for the attribution method, instead of the other way round. Besides, it also provides insight in implicit cash flows, when certain portfolio decisions are transferred to specialized managers. Keeping track of all the flows is one of the most important task performance professionals are faced with. Turning flows into returns is not as simple as one would expect. Especially, multi period and multi currency returns need ample consideration. The same holds for the notion of excess return. Once the return calculations have been established, you can turn to the selection of the attribution scheme. The focus is on the segmentation and the appropriateness of existing models. Taking all steps in this single framework enables you to meet the requirements of all target audiences.
References
- Allen G.C., “Performance Attribution for global Equity Portfolios”, Journal of Portfolio Management, Fall 1991.
- Brinson, G. P., L. Randolph Hood and Gilbert L. Beebower, “Determinants of Portfolio Performance,” Financial Analyst Journal, July-August 1986.
- Brinson, G.P. and Fachler, N., “Measuring Non-US Equity portfolio performance”, Journal of Portfolio Management, Spring 1985.
- Burnie, J.S, Knowles J.A., and Teder T.J., “Arithmetic and Geometric Attribution”, Journal of Performance Measurement, Fall 1998.
- Cariño, D., “Combining Attribution Effects Over Time”, Journal of Performance Measurement, Summer 1999.
- Geenen J., Klok M., and Van de Burgt, E.M., “Currency Overlay Attribution: a Practical Guide”, The Journal of Performance Measurement, forthcoming
- Menchero, J.G., “An Optimized Approach to Linking Attribution Effects Over Time”, Journal of Performance Measurement, Fall 2001.
- Menchero, J.G., “A fully geometric approach to performance attribution”, Journal of Performance Measurement, Winter 2000/2001
- Singer, B.D. and Karnosky, D.S., “The General Framework for Global Investment Management and Performance Attribution”, Journal of Portfolio Management, Winter 1995.
Notes
- The authors wish to thank Elske van de Burgt for her very useful comments.
- Note, that the frequency is not determined by actual trading activities; not changing positions is also considered to be a decision. What is important is to correctly assess the update frequency of the strategy that is actually applied by the manager. This could be quite low in case of fundamental value managers, or very high in case of quant portfolios. Putting aside the practical consequences, this could even go as far as intra-day evaluation in case of day trading.
in VBA Journaal door Marten Klok (r) Lucas Vermeulen1 (l)
