Z-scores bedrijfstakpensioenfondsen 1998-2002 geanalyseerd

De eerste 5-jaars z-toets levert de eerste uitvallers; een herbezinning

 

Introductie

In april 1998 is de vrijstellingsregeling in het kader van de wet Bedrijfstakpensioenfondsen van kracht geworden. In deze wet worden de voorwaarden genoemd waaronder een onderneming vrijstelling kan verkrijgen voor de verplichting de uitvoering van het pensioenreglement onder te brengen bij het pensioenfonds van de gehele bedrijfstak, het zogenaamde bedrijfspensioenfonds (BPF). Eén van de gebruikte criteria betreft de kwaliteiten van het BPF als belegger. Indien het BPF gemiddeld een lager rendement behaalt dan de zelfgekozen benchmark (meestal een verzameling indices) dan kan de onderneming een beroep doen op de vrijstellingsregeling. De onderneming mag dan de uitvoering van de pensioenregeling onderbrengen in een eigen pensioenfonds of bij een concurrent van het BPF, bijvoorbeeld een verzekeringsmaatschappij.

Het beleggingsperformance-criterium van de vrijstellingsregeling is gebaseerd op een steekproef. Gedurende een aantal aanééngesloten jaren wordt het rendementsverschil, gecorrigeerd voor beleggingskosten, tussen de pensioenfonds-portefeuille en de benchmark gemeten. Het resultaat van deze steekproef is een schatting van het gemiddelde rendementsverschil gedurende de gehele looptijd van het contract tussen de onderneming en het BPF. De nauwkeurigheid van de schatting is afhankelijk van de fluctuatie van de jaarlijkse rendementsverschillen (het actieve risico). Het met deze fluctuatie genormeerde rendementsverschil wordt de z-score genoemd. Omdat de steekproef slechts een schatting geeft van de gezochte z-score wordt een veiligheidsmarge ingebouwd. Pas als de z-score onder de kritische grens van –1,28 uitkomt, valt met 90% zekerheid te concluderen dat het BPF onvoldoende beleggingskwaliteiten heeft.

Recent zijn de resultaten van de steekproef over de eerste meetperiode (vanaf mei 1998 tot en met december 2002) beschikbaar gekomen. Op grond van deze cijfers vervalt de verplichtstelling bij twee bedrijfstakpensioenfondsen. De vraag is echter, of in het geval van deze pensioenfondsen de conclusie gerechtvaardigd is dat hun beleggingskwaliteiten te wensen over laten. In een voorgaand artikel (VBA journaal, december 2002, nr.3) hebben wij al stevige kritiek geleverd op de inrichting en uitvoering van de beleggingsperformancetoets. In deze bijdrage zullen wij aantonen dat volgens een statistisch betrouwbaardere methode (t-score toets) niet mag worden geconcludeerd dat de outperformance van de gezakte pensioenfondsen onvoldoende is. Daarbij zullen we allereerst de resultaten presenteren van de z-scores over 2002 en de consquenties daarvan voor de z-score toets over 1998-2002. Daarna zullen we door middel van verschillende analyses mogelijke effecten en verklaringen in beeld brengen. Specifiek wordt gekeken naar effecten op fondsniveau, effecten van de marktsituatie in 2002 en technische effecten van de z-score methodiek. Deze laatste analyse leidt tot het pleidooi om voor de beleggingsperformance-toets een t-score te gebruiken in plaats van een z-score.

 

Berekening van de z-score

De beleggingsperformancetoets is gericht op de jaarlijkse outperformance van de beleggingsportefeuille van een pensioenfonds ten opzichte van de zelfgekozen benchmark. De toets heeft tot doel, met een betrouwbaarheid van 90%, vast te stellen of een bedrijfstakpensioenfonds een gemiddelde outperformance heeft die tenminste gelijk is aan 0%. Hier hoort een minimale z-score bij van –1,28. De toets over 1998 t/m 2002 wordt volgens onderstaand schema berekend:

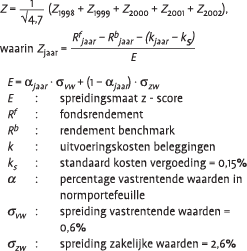
In de teller van de z-score staat de outperformance per jaar na kosten, waarbij een standaard kostenvergoeding van 15 basispunten meegenomen wordt. De standaardafwijkingen voor vastrentende waarden en zakelijke waarden die mee worden genomen in de beleggingsperformancetoets zijn gebaseerd op de rendementen van deze beleggingscategorieën van een selectie van pensioenfondsen (het WM-universum) in de periode 1992 tot 1996. De spreidingsmaat “E” is afhankelijk van de samenstelling van de beleggingsportefeuille van de geselecteerde pensioenfondsen, maar niet van de actuele spreiding van rendementen binnen aandelen en vastrentende waarden van het individuele fonds. De eerste toets gaat over 4,7 jaar aangezien de toets pas lopende het jaar 1998 is ingevoerd.

 

Resultaten z-score toets 1998-2002

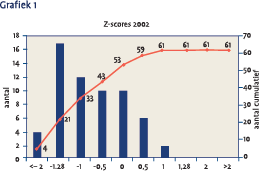
Het gemiddelde absolute rendement van Nederlandse ondernemings- en bedrijfspensioenfondsen in het jaar 2002 was –8,1%2. Het lage rendement is vooral het gevolg een grote weging in aandelen bij sterk dalende aandelenbeurzen. Hoe is het de bedrijfstakpensioenfondsen vergaan inzake hun actieve beleid?

Van de 61 fondsen waarvan de cijfers beschikbaar zijn3 hebben er 53 fondsen een z-score over 2002 behaald van minder dan 0. De kritische waarde van –1,28 wordt door 21 fondsen onderschreden (ruim 1/3 van het aantal bedrijfstakpensioenfondsen). Gemiddeld was de bijdrage van actief beleid met een zscore van –0,9 sterk negatief in 2002. Als we uitgaan van een gemiddelde beleggingsmix met 50% zakelijke waarden en 50% vastrentende waarden aan het begin van 2002, dan zou de gemiddelde underperformance ten opzichte van de eigen benchmark ongeveer –1,5% zijn. Dit komt overeen met een vermogensverlies van ca. –4,5 miljard euro voor de gehele groep.

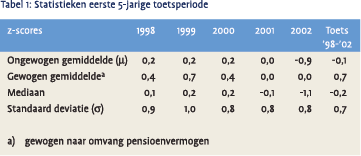In tabel 1 worden de belangrijkste statistieken over de eerste 5-jarige toetsperiode op een rijtje gezet.

Met de sterk negatieve resultaten in 2002 is eveneens de gemiddelde z-score over de 5-jaars periode negatief geworden (-0,1). Voor het eerst zijn 2 bedrijfstakpensioenfondsen gezakt voor de toets, met een z-score over 1998-2002 die kleiner is dan –1,28. Hiermee zouden werkgevers in de betreffende bedrijfstakken kunnen besluiten om naar een andere uitvoerder over te stappen4.

De vraag dringt zich op of nu gesteld mag worden dat bedrijfspensioenfondsen slechte uitvoerders zijn of dat er wellicht andere elementen een rol spelen voor de verklaring van de waargenomen lage z-scores.

 

Analyses z-scores 1998-20025

Fonds analyses

“Big is beautiful”

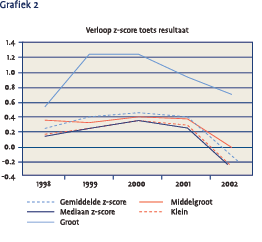
De grote bedrijfspensioenfondsen (met meer dan 5 miljard euro belegd vermogen) hebben een significant hogere z-score laten zien dan de overige bedrijfstakpensioenfondsen (gemiddeld 0,7 versus –0,1 totaal gemiddeld). De gemiddelde marktomvang-gewogen z-score ligt dan ook hoger dan het ongewogen gemiddelde (0,6 versus –0,1). Dit is een bevestiging van de eerdere resultaten.

In grafiek 2 staan de z-score toetsresultaten zoals die in de afgelopen jaren zijn opgebouwd. In 1998 is het cijfer gebaseerd op 0,7 jaar, in 1999 op 1,7 jaar tot en met 2002 waarin het cijfer is gebaseerd op 4,7 jaar. Uit de grafiek blijkt het duidelijk afwijkende resultaat van de grote fondsen. De middelgrote fondsen zitten in de buurt van het gemiddelde en de kleine fondsen zitten daar duidelijk onder. Een deel van de verklaring zou kunnen liggen in het hogere kostenniveau dat een klein pensioenfonds heeft, of wellicht het ontbreken van professioneel risicomanagement. Overigens is het interessant dat met name kleinere fondsen vaker hun beleggingen geheel hebben uitbesteed6.

Uitvallers

Als alle fondsen gemiddeld een z-score van 0 zouden halen, waarbij de standaarddeviatie van de z-scores gelijk zou zijn aan 1, dan zouden we moeten verwachten dat het aantal uitvallers ca. 10% zou zijn van het aantal fondsen. Dit is niet het geval. Er zijn 2 uitvallers, waar je onder de aanname 6 fondsen zou mogen verwachten. Hier kan overigens niet uit worden afgeleid dat de (overige) fondsen het goed doen, omdat de gemaakte aanname voor de spreiding onjuist is (zie verderop bij “problemen in techniek zscore meting”).

Gezien de huidige z-scores, die een tijdlang worden meegedragen (“rolling horizon” principe) zal na de meting over 2003 het aantal uitvallers vrijwel met zekerheid toenemen. De grote klap komt waarschijnlijk als met het vervallen van de jaren 1998 en 1999 het positieve invoeringseffect geheel is uitgewerkt7. Zeer waarschijnlijk zal (additioneel) 1 fonds over 2003 de toets niet halen, gezien een te behalen z-score van minimaal +0,9 in het jaar 2003. Dit vergt een uitzonderlijk goede beleggingsprestatie. Daarnaast is er een fonds dat over 2 jaar een gemiddelde z-score moet halen van +0,3, gezien het feit dat twee goede jaren wegvallen. Als dat lukt, dan zal ook het jaar er na een z-score van minimaal 0,4 behaald moeten worden. Voor zes fondsen geldt dat over de komende 2 jaar gemiddeld een z-score van 0 behaald moet worden. Kortom er zijn voor de komende jaren uitvallers te verwachten. Als een gemiddelde score zoals over het jaar 2002 zich nogmaals voordoet, zal het aantal uitvallers zelfs fors toenemen.

Marktgerelateerde analyses – Het is gegeven de beschikbare data moeilijk vast te stellen of gemeten rendementsverschillen het gevolg zijn van asset allocatie (wegings) beslissingen of van selectie beslissingen. We zullen hier zowel een oorzaak zoeken in de wegingen (specifiek in 2002) als in de selectie-resultaten (1998-2002).

Rebalancing

Onder rebalancing verstaan wij hier het terugbrengen van de wegingen van beleggingscategorieën in de portefeuille naar de (oorspronkelijke) strategische (benchmark) gewichten. Door de grote koersuitslagen zijn “verkeerde” beslissingen in 2002 hard afgestraft. Vermogensbeheerders die in de eerste helft van 2002 nog in spoedig economisch herstel geloofden en zowel de aandelenweging verhoogde als de duration van de obligaties verlaagden, verloren veel ten opzichte van de benchmark. Niet alleen daalden de aandelenkoersen tot een niet waarschijnlijk geacht laag niveau, maar doordat de obligaties als vluchthaven werden gebruikt daalde tevens de kapitaalmarktrente tot een historisch laag niveau. Wellicht geschrokken van de resultaten in de eerste negen maanden van 2002 was men in het laatste kwartaal naar alle waarschijnlijkheid te voorzichtig waardoor niet voldoende van het herstel van de beursen kon worden geprofiteerd (zie grafiek 3: verloop aandelenrendement in 2002).

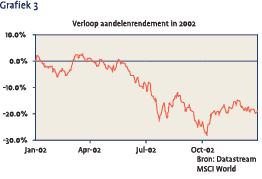Bovendien zijn in het jaar 2002 de aandelenbeurzen zodanig omlaag gegaan dat de dekkingsgraad van vele fondsen in de buurt van de 100% terecht is gekomen. De toezichthouder, de PVK, heeft dit met zorg aangezien en heeft op 30 september een brief naar de pensioenfondsen gestuurd waarin ze explicieter dan ooit te voren heeft aangegeven hoe (strikt) er tegen de solvabiliteitseisen aangekeken zou moeten worden. Onder andere bleek hieruit dat fondsen met een dekkingsgraad lager dan 105% al een dekkingstekort hebben dat op korte termijn moet worden aangevuld. Besturen zagen zich voor de vraag gesteld wanneer in te grijpen door aanpassing van de beleggingsmix, naast eventuele maatregelen (voor 2003) inzake indexatiebeleid en premiebeleid. Zeker als het pensioenfonds bijvoorbeeld een maandelijkse rebalancing-frequentie hanteerde kan, bij sterk dalende aandelenkoersen, de discipline in dezen onder druk zijn komen te staan. Doordat de aandelenkoersen niet monotoon daalden kan zo’n beslissing op het verkeerde moment pijnlijke gevolgen hebben gehad voor de z-score.

We zullen dit demonstreren met een voorbeeld. Als het bestuur heeft besloten om na het eerste halfjaar met een sterk negatief aandelenrendement te rebalancen naar de strategische gewichten aan het begin van het jaar, ook al gaat de z-score benchmark uit van niet rebalancen, dan geeft dat zo maar 0,5%punt extra negatief rendement.

Andersom als een bestuur besluit niet te rebalancen na de eerste negen maanden, terwijl de z-score benchmark wel uit gaat van rebalancen, levert dat zo maar 0,3%punt negatieve performance ten opzichte van de benchmark op, gezien de oplopende koersen in het laatste kwartaal.

Gezien de hiervoor beschreven dilemma’s is het overigens evident dat er een spanning kan bestaan tussen de wettelijk voorgeschreven z-score toets en de richtlijnen die de PVK uitvaardigt. Pensioenfondsen die tijdens het jaar 2002 op basis van de geëxpliciteerde richtlijnen van de PVK hun beleggingsmix hebben aangepast, en dit niet konden doen voor de z-score benchmark, en daardoor een negatief effect op hun z-score hebben opgelopen, zouden hier een goed argument hebben tegen een strakke hantering van de z-score regeling. De ‘correlatie’ tussen de verschillende wettelijke kaders zou hier wel eens –1 kunnen zijn.

Hoge correlatie tussen absolute en actieve risico’s?

De correlatie van de absolute aandelenrendementen en de gewogen z-scores is met ruim 0.8 hoog. Dit zou er op kunnen wijzen dat het absolute en relatieve rendement op aandelen met elkaar samenhangen. In jaren dat aandelen negatief scoren (2000 t/m 2002) is dit slecht nieuws. Interessant is de vraag of het actieve aandelenrendement verklaard wordt door selectie (alfa) of door een hoger marktrisico (beta). Indien dit laatste punt het geval is, dan zou nog eens goed naar de kosten van actief management moeten worden gekeken. Dit, aangezien meestal wordt getracht aandelenmanagers te selecteren op grond van de mogelijk positieve alfa die zij kunnen leveren en daar ook naar betaald willen worden. De beslissing om meer of minder marktrisico te nemen (beta) is een allocatie beslissing en eenvoudig en goedkoop te implementeren.

Problemen in techniek z-score meting – Al eerder is gewezen op de technische onvolkomenheden in de z-score meting. In onze analyses van de z-score toets over 1998 tot en met 2001 (VBA journaal, december 2002) zijn hier zowel theoretische als praktische bezwaren genoemd. We zullen hier ingaan op het mogelijke probleem van laag correlerende benchmarks alsmede de effecten van de spreidingsmaat E.

Laag correlerende benchmarks

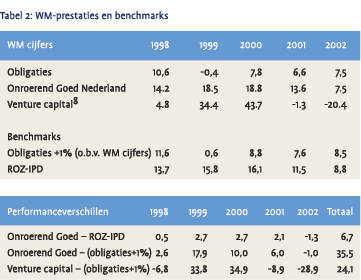
Benchmarks die slecht correleren met de bijbehorende beleggingscategorie hebben mogelijk een significant effect gehad op de gemeten z-scores. Als er geen goede benchmark is voor een categorie, dan moet volgens de vrijstellingsrichtlijn het rendement van een rente-index worden gebruikt vermeerderd met 1%-punt rendement. Er zijn meerdere categorieën waar dit op toegepast kan worden zoals direct onroerend goed en private equity. Om de effecten hiervan te analyseren hebben we gebruik gemaakt van de WM rendementen van de verschillende asset categorieën (zie tabel 2).

Als fondsen ten aanzien van de categorie onroerend goed het rendement van een rente benchmark + 1% hebben gehanteerd in plaats van bijvoorbeeld de ROZ/IPD index dan heeft dat over 1998 t/m 2002 een positieve invloed gehad op de z-score.

Indien 50% van de pensioenfondsen met een gemiddelde gewicht onroerend goed van 10%9 de rente benchmark heeft gehanteerd, dan heeft dat op de gemiddelde z-score van alle bedrijfstakpensioenfondsen over de gehele periode 1998-2002 een positief effect gehad van +0,5. Zouden we de z-score hiervoor corrigeren dan resteert een gemiddelde z-score van –0,6.

Eenzelfde redenatie gaat op voor de categorie venture capital. Als alle fondsen hier een rente benchmark voor gebruikt hebben bij een gemiddelde weging van 1%, gaf dat tot 2001 een positieve bijdrage aan de zscore van +0,2. In 2002 is dit totale effect teniet gedaan, zodat cumulatief de bijdrage uitkomt op 0. Overigens is de correlatie van de gewogen z-scores met de venture capital scores (+0,9) hoog.

Bedrijfspensioenfondsen kunnen in hun beleggingsportefeuille een strategische holding in de eigen uitvoeringsorganisatie meenemen. Ook hiervoor gelden dezelfde opmerkingen als voor private equity en onroerend goed.

Per saldo hebben de bedrijfstakpensioenfondsen tot nu toe de wind meegehad en heeft het geconstateerde benchmarkeffect in de jaren 1998 – 2002 gunstig voor ze uitgepakt. Maar, zoals de rendementen op venture capital en onroerend goed in het jaar 2002 laten zien kan het effect even goed een negatieve uitwerking hebben op de z-score.

Effecten van spreidingsmaat E

Op basis van slechts 5 z-scores per pensioenfonds kan per individueel fonds niet veel worden geconcludeerd, toch zijn er wel een aantal interessante waarnemingen te doen. De gemiddelde standdaarddeviatie van de 5 zscores per fonds, is ten opzichte van vorig jaar (4 waarnemingen 1998-2001) toegenomen van 0,7 naar 0,9. De uitslagen in 2002 zijn zodanig groot, dat als we passief beleggen opvatten als een kleine standaarddeviatie van de z-scores ten opzichte van 0, bijvoorbeeld kleiner dan 0,2 (vergelijkbaar met een tracking error van circa 0,4%), er van de 61 pensioenfondsen geen enkele meer als puur passief kan worden aangemerkt (i.t.t. 2001). De laagste waarneming voor deze maat is 0,5. Fondsen met een kleine standaard deviatie van de rendementen hebben een grotere kans te slagen voor de toets, omdat het actief risico veel lager is dan de gebudgetteerde spreidingsmaat E (deze is minimaal 0,6 en gemiddeld 1,6). Aan de andere kant van het spectrum hebben 15 van de 61 pensioenfondsen een standaarddeviatie van de z-score van groter dan 1. Dit zou er op kunnen wijzen dat ze een grotere spreiding in resultaten kennen dan die is meegenomen in de zscore. Om het risico op zakken voor de z-score toets te beperken zullen deze fondsen een gemiddelde, voor kosten gecorrigeerde, outperformance op hun eigen normportefeuille moeten behalen hoger dan de vereiste 0%. Deze fondsen lopen dus een relatief grotere kans op het niet halen van de z-score toets in de toekomst.

De spreidingsmaat E is niet fondsspecifiek en enigszins willekeurig, aangezien deze wordt gebaseerd op de historische volatiliteit van het WM Universum. De waargenomen spreiding in het WM universum over 1998 tot en met 2002 (5 jaar) is voor aandelen 1,4% (2002: 2,6%) en voor vastrentende waarden 0,5% (2002: 0,6%). Uitgaande van een 50% weging in aandelen voor het gemiddelde fonds zou op basis van deze cijfers de spreidingsmaat E 0,95% zijn (2002: 1,6%). Als deze toegepast zou zijn voor de huidige toets, dan zouden 7 fondsen de toets niet hebben gehaald. Daarnaast daalt de gemiddelde z-score van –0,1 naar –0,2 en stijgt de standaarddeviatie van de zscores tot 1,1. Als voor de toets over 2003 deze nieuwe spreidingsmaatstaven zouden worden ingevoerd, dan staat voor een groot aantal fondsen het water aan de lippen.

De werkelijke spreiding in de outperformances is lager dan de in de z-score toets gebruikte spreidingsmaat E. De gemiddelde standaarddeviatie van de zscores per jaar is kleiner dan 1 (namelijk 0,8). Dit betekent de facto dat de meeste fondsen minder risico nemen dan mee wordt genomen in hun spreidingsmaat E. Een belangrijke oorzaak hiervan is de in de spreidingsmaat veronderstelde perfecte correlatie tussen zakelijke waarden en vastrentende waarden. Als bij de berekening van de te gebruiken spreidingsmaat in de z-score toets rekening wordt gehouden met een correlatie van 0, dan komt de berekende spreiding meer overeen met de waargenomen spreiding in z-scores.

De hierboven beschreven waarnemingen geven nogmaals aan dat de spreidingsmaat E die wordt meegenomen omstreden is en eveneens een significant effect heeft op de z-scores. Hierna onderzoeken we de mogelijkheid om te komen tot een aanpassing van de z-score toets, zodanig, dat een aantal van de genoemde nadelen/effecten worden weggenomen en er sprake kan zijn van een reëlere toets.

 

Een mogelijk alternatief: de t-score toets

Statistische achtergrond – Door al het rumoer dat ieder jaar weer ontstaat na de publicatie van de jaarlijkse z-scores, wordt wel eens vergeten dat strikt statistisch er geen sprake is van een jaarlijkse zscore. Een z-score-toets wordt gebruikt om een (nul)hypothese betreffende een populatie te testen. In het geval van de beleggingsperformancetoets is de populatie de verzameling jaarlijkse verschillen tussen het rendement behaald met de feitelijke beleggingsportefeuille van het pensioenfonds en het theoretische rendement van de normportefeuille. De nulhypothese luidt: “het gemiddelde jaarlijkse rendementsverschil is tenminste 0%”. De hypothese wordt getest door middel van een steekproef (5 jaar rendementsverschillen) waarvan het gemiddelde aan het z-score criterium wordt onderworpen. Indien het genormaliseerde10 gemiddelde, de z-score, van de steekproef lager is dan een vooraf gekozen grens, kan de nulhypothese met een bepaalde zekerheid worden verworpen. Het blijft namelijk statistisch mogelijk dat het steekproefgemiddelde onder de kritische grens uitkomt terwijl het gemiddelde van de populatie wel positief is. Maar, omdat er gewerkt wordt met een beperkte steekproef kan geen 100% zekerheid verkregen worden. Strikt genomen is de z-score van een pensioenfonds dus het genormaliseerde gemiddelde van de rendementsverschillen die gemeten zijn in de steekproef. Er mag niet geconcludeerd worden dat een pensioenfonds met een z-score in de periode 1998-2002 van –0,5% het slecht heeft gedaan omdat pas bij een z-score van minder dan –1,28% de nulhypothese verworpen mag worden. Ondanks een zscore van –0,5% is het statistisch heel goed mogelijk (ca. 30% kans) dat de gemiddelde outperformance in de populatie (dus de lange termijn) hoger is dan 0%.

Van z-score naar t-score – Bij het gebruik van een z-score toets om een nulhypothese te testen wordt verondersteld dat de standaarddeviatie van de populatie bekend is. In de z-score toets in het kader van de wet BPF wordt hiervoor de spreidingsmaat E gebruikt. Een deel van de kritiek op de beleggingsperformance toets richt zich juist op deze E. Dat E geen goede schatting is van de standaarddeviatie in de populaties blijkt ook uit de standaarddeviaties van de gemeten z-scores. Omdat het genormaliseerde rendementen betreft zou men verwachten dat deze standaarddeviatie gelijk is aan 1.

De z-scores1998 – 2002 hebben echter een standaarddeviatie van ca. 0,7%. Het ligt daarom meer voor de hand in de performancetoets een t-score criterium te gebruiken. In een t-score toets wordt geen gebruik gemaakt van de standaarddeviatie van de populatie (omdat deze niet bekend is). In plaats daarvan wordt de standaarddeviatie van de resultaten in de steekproef gebruikt (zie kader).

Omdat de t-verdeling die ten grondslag ligt aan de t-score een andere vorm heeft dan de normaalverdeling die verondersteld is in een z-score toets, heeft de kritieke grens bij een betrouwbaarheidsinterval van 90% een andere waarde dan –1,28%, bij een steekproefgrootte van 5 is de kritieke grens gelijk aan –1,53.

Omdat naarmate het aantal trekkingen in de steekproef toeneemt de t-verdeling meer op een normaalverdeling gaat lijken, schuift de kritieke grens bij toenemende steekproefgrootte op naar –1,28 (n=20: -1,33).

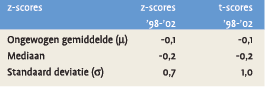Resultaten – Onder veronderstelling dat de spreidingsmaat E per pensioenfonds in de jaren 1998 – 2002 vrijwel constant is geweest, kunnen uit de gepubliceerde z-scores de t-scores berekend worden11. In onderstaande tabel worden een aantal karakteristieken van de op deze wijze berekende t-scores naast die van de z-scores geplaatst.

Het is bij vermogensbeheer gebruikelijk om de vergoeding die is verkregen voor een gelopen risico te waarderen door deze uit te drukken per eenheid risico. Zo relateert de Information Ratio (IR) de behaalde outperformance (OP) aan de Tracking Error (TE). In formulevorm IR = OP / TE. Hoe hoger de Information Ratio, hoe hoger de vergoeding per risico eenheid, hoe beter de prestatie van de uitvoerder. Negatieve Information Ratio’s zijn het gevolg van underperformance 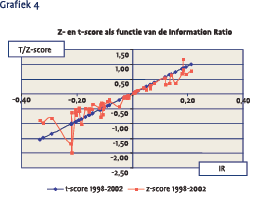en daarom niet goed. Echter ook in het geval van underperformance is de Information Ratio een nuttige parameter om de behaalde underperformance in perspectief te zetten. Indien er veel risico is genomen (hoge TE) mag de underperformance op basis van dezelfde veronderstelde beleggingsdeskundigheid hoger uitvallen dan wanneer er minder risico is genomen.

In grafiek 4 zijn zowel de z-scores1998 -2002 als de t- scores1998 -2002 uitgezet als functie van de Information Ratio, zoals deze is berekend uit de z-scores in de periode 1998 – 2002. Wat opvalt in de grafiek is dat de t-score een eerlijkere maat lijkt op basis van de rendements/risico-verhouding, dan de z-score. De twee pensioenfondsen die gezakt zijn voor de z-score toets blijken, als gevolg van de relatief hoge TE, met hun t-score nog voldoende ver verwijderd van de kritische grens en slagen makkelijk voor de t-score toets. Voor drie andere fondsen, die dankzij een lage TE wel slaagden voor de z-score toets, is het in de tscore toets kantje boord. Bij deze drie pensioenfondsen liggen de t-scores vlak bij de grens van –1,53%.

 

Conclusie

De z-score toetsing over de periode 1998-2002 heeft geleid tot de eerste twee uitvallers. Deze blijken met name te veel risico versus de standaardmaat E te hebben genomen, waardoor automatisch een grotere kans op het niet halen van deze toets werd gelopen. Bij gelijkblijvende methode van meting lijkt het zeker dat er de komende jaren meer uitvallers komen.

De vele negatieve resultaten over 2002 (ruim 85% van de fondsen) moeten wellicht worden toegeschreven aan de (vooralsnog) exceptionele aandelenrendementen die hebben geleid tot beleidswijzigingen en aanpassingen in de rebalancing strategie. Hierbij lijkt het dat de wettelijke kaders inzake de z-score toets en de kaders die de PVK aanreikt, met elkaar op gespannen voet staan. Er kunnen significante uitslagen in de z-score toets zich voordoen als gevolg van beleidsingrepen op grond van richtlijnen van de PVK.

Grote fondsen halen goede z-scores. De vraag voor de komende jaren is of het significante verschil tussen grote en kleine fondsen gehandhaafd blijft. Indien dit consistent blijkt te blijven zou dit consequenties kunnen krijgen ten aanzien van de uitvoering van de kleine fondsen.

Aan de z-score kleven een aantal theoretische en praktische nadelen, waardoor de uitkomsten enigszins willekeurig zijn. Hierdoor is het lastig om vast te stellen of bedrijfspensioenfondsen het over het geheel al dan niet goed doen. Laagcorrelerende benchmarks kunnen een per saldo positief effect hebben gehad op de z-score over de afgelopen jaren. In de toekomst kan dit effect zich echter ook negatief manifesteren. Aan de spreidingsmaat E kleven nogal wat nadelen. Indien bijvoorbeeld de methodiek tot vaststelling van de spreidingsmaat E wordt gehandhaafd en de WM cijfers over 1998-2002 worden gebruikt in plaats van tot op heden gehanteerde WM cijfers over 1992-1996, leidt dit tot een groot aantal uitvallers. Dit geeft aan dat de methodiek, die van verschillende kanten reeds theoretisch is bekritiseerd, hiermee cijfermatig ook nog eens door de mand valt. Mocht deze methodiek toch blijvend worden toegepast, dan rest bedrijfspensioenfondsen slechts om passiever te beleggen.

Een betere methodiek zou gebaseerd kunnen worden op de standaard deviaties van de steekproef in plaats van die van de populatie, waarbij de z-score toets wordt vervangen door een t-score toets. Hiermee zou meer recht worden gedaan aan een goede verhouding tussen rendement en risico, alsmede worden pensioenfondsen niet voor een te groot risico bestraft. Toegepast op 1998-2002 betekent dit dat de 2 voor de z-score toets gezakte fondsen ruim geslaagd zijn voor de t-score toets, maar dat 3 andere fondsen bijna door de mand vallen.

 

Informatiebronnen

• Braker, JGB, “Pensioenfondsen leggen de lat te hoog”, ESB, nr. 4396 (jaargang 87), 7 maart 2003, pagina 103-104.
• Molenkamp, J.B., Zweekhorst C., “Prestaties bedrijfstakpensioenfondsen geanalyseerd; de z-score zegt niet alles”, VBA journaal, december 2002, nr.3., pagina 24-30.
• VB, VB contact, nr. 170 april 2002
• VB, z-scores 2002, maart 2003
• The WM Company, “ Performance analytics, Nederland-Jaaroverzicht 2002”, 2003.

Noten

1. Jan Bertus Molenkamp is werkzaam bij Mn Services en verbonden aan de Vrije Universiteit te Amsterdam. Kees Zweekhorst is werkzaam bij AON Consulting.
2. WM universum van Nederlandse pensioenfondsen 2002
3. Op basis van cijfers van de VB. In vergelijking met ons vorige onderzoek is het aantal van 63 naar 61 gegaan. Van 2 vroegpensioenfondsen hebben we geen cijfers over 2002 en over de toetsperiode 1998-2002. Gebleken is dat bij veel pensioenfondsen de Z-scores van vorige jaren nog worden aangepast. De gemiddelde aanpassing is per saldo licht positief, maar heeft geen significant effect.
4. In ons vorige artikel is reeds aangegeven dat de beslissing om weg te gaan bij het bedrijfstakpensioenfonds niet zo snel genomen zal worden. Dit heeft los van zaken als service, etc., te maken met de vraag welk bedrag men meekrijgt als de verplichtingen elders worden ondergebracht.
5. De analyses die kunnen worden verricht op de z-scores van de bedrijfspensioenfondsen zijn cross-sectioneel en de conclusies die daaruit kunnen worden getrokken hebben dan ook geen betrekking op individuele fondsen.
6. De uitvoering is dus niet per definitie door een bedrijfspensioenfonds, maar kan ook bij een bank of verzekeraar ondergebracht zijn. Het ironische hiervan is dat verzekeraars met name marktwerking in de bedrijfspensioenfonds sector willen bevorderen en dat ze ook een oorzaak kunnen zijn van het feit dat een bedrijfspensioenfonds de z-score toets niet haalt.
7. In ons vorige artikel is onderbouwd dat er mogelijk sprake is van een positief invoeringseffect in de jaren 1998 en 1999. Dit zou mogelijk te maken hebben met het (op)waarderen van illiquide beleggingen naar marktwaarde.
8. In ons vorige artikel hebben we hier alternatieve beleggingen gebruikt. Die categorie is echter nog “vervuild” met zaken als commodities, waar wel goede benchmarks voor zijn, en die bijv. In 2002 een erg hoog rendement kenden.
9. Schatting op basis van cijfers van The WM Company.
10. Normaliseren houdt in dit geval in dat de in de steekproef gemeten outperformances gedeeld worden door de veronderstelde standaarddeviatie van de populatie (E).
11. t = , met s = standaarddeviatie van de jaarlijkse z-scores.

 

1 July 2003 in VBA Journaal door Jan Bertus Molenkamp, Kees Zweekhorst